题目内容
设一次函数f（x）为函数F（x）的导数，若存在实数x0∈（1，2），使得f（-x0）=-f（x0）＜0，则不等式F（2x-1）＜F（x）的解集为 ．
考点：导数的运算
专题：导数的概念及应用
分析：首先判断出f（x）为奇函数，令f（x）=2ax（a＞0），根据条件列出不等式，解得即可．
解答：
解：由存在实数x0∈（1，2），使得f（-x0）=-f（x0）＜0，
∴f（x）为奇函数，
令f（x）=2ax（a＞0），
∴F（x）=ax2，
∵F（2x-1）＜F（x）
∴F（2x-1）-F（x）=a（2x-1）2-ax2=a（3x-1）（x-1）＜0
即（3x-1）（x-1）＜0，
解得，
＜x＜1．
故答案为：(
，1)
∴f（x）为奇函数，
令f（x）=2ax（a＞0），
∴F（x）=ax2，
∵F（2x-1）＜F（x）
∴F（2x-1）-F（x）=a（2x-1）2-ax2=a（3x-1）（x-1）＜0
即（3x-1）（x-1）＜0，
解得，
| 1 |
| 3 |
故答案为：(
| 1 |
| 3 |
点评：本题主要考查了函数的奇偶性，以及不等式的解法，属于基础题．
练习册系列答案
相关题目
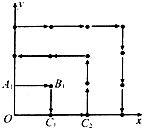某地区为了绿化环境进行大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在点Al（0，1），第二棵树在点B1（1，1），第三棵树在点C1（1，0），第四棵树在点C2（2，0），接着按图中箭头方向每隔一个单位种一棵树，那么：
若x∈（-设集合U={（x，y）|x∈R，y∈R}，A={（x，y）|2x-y+m＞0}，B={（x，y）|x+y-n≤0}，若P（2，3）∈A∩（∁UB），则（ ）
| A、m＞-1且n＜5 |
| B、m＜-1且n＜5 |
| C、m＞-1且＞5 |
| D、m＜-1且n＞5 |