题目内容
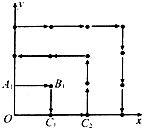 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么:
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么:(1)第n棵树所在点坐标是(44,0),则n=
(2)第2014棵树所在点的坐标是
考点:归纳推理
专题:推理和证明
分析:(1)将OA1B1C1设为第一个正方形,种植3棵树,依次下去,归纳出第二个正方形,第三个正方形种植的棵树,由第n棵树所在点坐标是(44,0),可求n;
(2)由(1)可知正方形种植的树,它们构成一个等差数列,公差为2,计算出前43个正方形共有多少棵树,从而得到第2014棵树所在的点的坐标.
(2)由(1)可知正方形种植的树,它们构成一个等差数列,公差为2,计算出前43个正方形共有多少棵树,从而得到第2014棵树所在的点的坐标.
解答:
解:(1)OA1B1C1设为第一个正方形,种植3棵树,依次下去,第二个正方形种植5棵树,第三个正方形种植7棵树,由第n棵树所在点坐标是(44,0),则n=3+5+7+…+89-1=1936;
(2)由(1)可知正方形种植的树,它们构成一个等差数列,公差为2.
故前43个正方形共有43×3+
×2=1935棵树,
又2014-1935=79,79-44=35,45-35=10,
因此第2014棵树在(10,44)点处.
故答案为:(1)1936 (2)(10,44)
(2)由(1)可知正方形种植的树,它们构成一个等差数列,公差为2.
故前43个正方形共有43×3+
| 43×42 |
| 2 |
又2014-1935=79,79-44=35,45-35=10,
因此第2014棵树在(10,44)点处.
故答案为:(1)1936 (2)(10,44)
点评:本题考点是进行简单的合情推理,由图形观察出规律是解题的重点.

练习册系列答案
相关题目
