题目内容
已知函数f(x)=ax-
,且atf(2t)+mf(t)≥0,求m的值.
| 1 |
| ax |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:由已知条件得at(a2t-
)+m(at-
)≥0,从而得到m(at-
)≥
-a3t,再由at-
的符号进行分类讨论,由此能求出结果.
| 1 |
| a2t |
| 1 |
| at |
| 1 |
| at |
| 1 |
| at |
| 1 |
| at |
解答:
解:∵f(x)=ax-
,且atf(2t)+mf(t)≥0,
∴at(a2t-
)+m(at-
)≥0,
∴m(at-
)≥
-a3t,
①当at-
=0,即at=±1时,m=0.
②当at-
>0,即at>1或at<-1时,
m>
=
=-a2t-1.
③当at-
=0,即-1<at<1时,
m<
=
=-a2t-1.
| 1 |
| ax |
∴at(a2t-
| 1 |
| a2t |
| 1 |
| at |
∴m(at-
| 1 |
| at |
| 1 |
| at |
①当at-
| 1 |
| at |
②当at-
| 1 |
| at |
m>
| ||
at-
|
| 1-a4t |
| a2t-1 |
③当at-
| 1 |
| at |
m<
| ||
at-
|
| 1-a4t |
| a2t-1 |
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意有理数指数幂的运算法则的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
盒子中装有编号为1,2,3,4,5,6,7,8,9的九个球,从中任意取出两个,则这两个球的编号之积为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
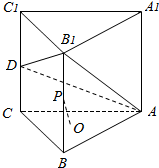 三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.
三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.