题目内容
9. 在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:①点E,F,G,H四点共面;
②直线EH,BD,FG相交于一点.
分析 ①利用三角形的中位线平行于第三边和平行线分线段成比例定理,
得到EF、GH都平行于AC,由平行线的传递性得到EF∥GH,
根据两平行线确定一平面得出证明;
(2)利用分别在两个平面内的点在这两个平面的交线上,即可证明.
解答 证明:①如图所示,
空间四边形ABCD中,H,G分别是AD,CD的中点,
∴HG∥AC;
又$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$,
∴EF∥AC,
∴EF∥HG,
E、F、G、H四点共面;
②设EH与FG交于点P,
∵EH?平面ABD
∴P在平面ABD内,
同理P在平面BCD内,
且平面ABD∩平面BCD=BD,
∴点P在直线BD上,
∴直线EH,BD,FG相交于一点.
点评 本题考查了三角形的中位线性质、平行线分线段成比例定理、直线的平行性的传递性、确定平面的条件以及三线共点的应用问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.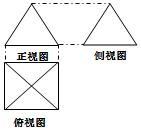 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )| A. | .$2\sqrt{3}$cm | B. | .$4\sqrt{3}$cm2 | C. | 8 cm2 | D. | 12 cm2 |
17.某电脑公司有6名产品推销员,其工作年限与年推销金额的数据如表:
(1)以工作年限为自变量,推销金额为因变量y,作出散点图;
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
1.已知半径为r的圆内切于某等边三角形,若在该三角形内任取一点,则该点到圆心的距离大于半径r的概率为( )
| A. | $\frac{\sqrt{3}π}{9}$ | B. | 1-$\frac{\sqrt{3}π}{9}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | 1-$\frac{\sqrt{3}π}{18}$ |
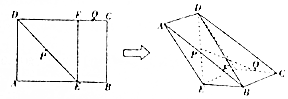 已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.
已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.