题目内容
不等式组
所表示的平面区域的面积为( )
|
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点:简单线性规划
专题:不等式的解法及应用
分析:画出不等式组
表示的平面区域为直角三角形ABC及其内部的部分,求得A、B、C各个点的坐标,可得直角三角形ABC的面积.
|
解答:
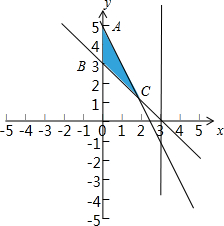 解:不等式组
解:不等式组
表示的平面区域为直角三角形ABC及其内部的部分,如图所示:
容易求得A(5,0),
B(3,0),由
解得
∴C(2,1),
不等式组
表示的平面区域的面积是三角形ABC的面积,即
×AB×xC=
×2×2=2,
故选:B.
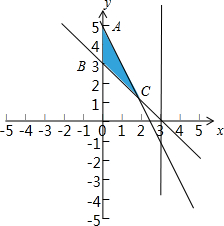 解:不等式组
解:不等式组
|
容易求得A(5,0),
B(3,0),由
|
|
∴C(2,1),
不等式组
|
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题主要考查二元一次不等式组表示平面区域,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图为与杨辉三角结构相似的“巴斯卡”三角,这个三角的构造方法是:除第一行为1外,其余各行中的每一个数,都等于它右肩上的数乘以右肩所在的行数,再加上左肩而得.例如第5行第3个数是35,它的右肩为6,左肩为11,右肩所在的行数为4,所以35=6×4+11.这个三角中的数与下面这个展开式中的系数有关:x(x+1)(x+2)…[x+(n-1)]=anxn+an-1xn-1+…+a1x,则在“巴斯卡”三角中,第8行从左到右的第2个数到第7个数之和为( )
如图为与杨辉三角结构相似的“巴斯卡”三角,这个三角的构造方法是:除第一行为1外,其余各行中的每一个数,都等于它右肩上的数乘以右肩所在的行数,再加上左肩而得.例如第5行第3个数是35,它的右肩为6,左肩为11,右肩所在的行数为4,所以35=6×4+11.这个三角中的数与下面这个展开式中的系数有关:x(x+1)(x+2)…[x+(n-1)]=anxn+an-1xn-1+…+a1x,则在“巴斯卡”三角中,第8行从左到右的第2个数到第7个数之和为( )| A、322559 |
| B、35279 |
| C、5880 |
| D、322560 |
中国古代数学著作《九章算法》中的“更相减损术”可用来求两个正整数的最大公约数.现应用此法求168与93的最大公约数:记(168,93)为初始状态,则第一步可得(75,93),第二步得到(75,18),第三步得到(57,18),第四步将得到( )
| A、(57,18) |
| B、(39,3) |
| C、(39,18) |
| D、(21,18) |
设椭圆
+
=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为B.若|BF2|=|F1F2|=2,则该椭圆的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={1,2,3,…,n}(n≥4),从集合A中取出4个不同的数构成有序数组(a1,a2,a3,a4),若对任意的2≤i≤4,都存在1≤j<i,使得|ai-aj|=1,则称该数组为“1-数组”.则“1-数组”共有( )
| A、4n-4个 | ||
| B、8n-24个 | ||
| C、2n(n-2)个 | ||
D、
|
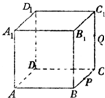 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.当CQ=