题目内容
15.已知动点P位于抛物线y2=4x上,定点An的坐标为($\frac{2}{3}$n,0)(n=1,2,3,4),则|$\overrightarrow{P{A}_{1}}$+$\overrightarrow{P{A}_{2}}$|+|$\overrightarrow{P{A}_{3}}$+$\overrightarrow{P{A}_{4}}$|的最小值为( )| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | 2 |
分析 根据向量坐标的运算以及向量模长公式,结合抛物线的性质,利用构造法转化为抛物线上的点到两点之间的距离和的最值问题进行求解即可.
解答 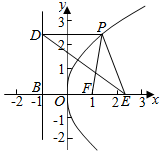 解:设P(x,y),则y2=4x,
解:设P(x,y),则y2=4x,
则$\overrightarrow{P{A}_{1}}$+$\overrightarrow{P{A}_{2}}$=($\frac{2}{3}$-x,-y)+($\frac{4}{3}$-x,-y)=(2-2x,-2y),$\overrightarrow{P{A}_{3}}$+$\overrightarrow{P{A}_{4}}$=(2-x,-y)+($\frac{8}{3}$-x,-y)=($\frac{14}{3}$-2x,-2y),
则|$\overrightarrow{P{A}_{1}}$+$\overrightarrow{P{A}_{2}}$|+|$\overrightarrow{P{A}_{3}}$+$\overrightarrow{P{A}_{4}}$|=$\sqrt{(2-2x)^{2}+4{y}^{2}}$+$\sqrt{(\frac{14}{3}-2x)^{2}+4{y}^{2}}$=2($\sqrt{(x-1)^{2}+{y}^{2}}$+$\sqrt{(x-\frac{7}{3})^{2}+{y}^{2}}$)
设P(x,y),F(1,0),F($\frac{7}{3}$,0),
则$\sqrt{(x-1)^{2}+{y}^{2}}$表示P到F点的距离PF,
$\sqrt{(x-\frac{7}{3})^{2}+{y}^{2}}$表示P到E的距离PE
则过P作PD⊥准线l,
则PD=PQ,
则PE+PF=PD+PE≥BE=$\frac{7}{3}$-(-1)=$\frac{10}{3}$,
即|$\overrightarrow{P{A}_{1}}$+$\overrightarrow{P{A}_{2}}$|+|$\overrightarrow{P{A}_{3}}$+$\overrightarrow{P{A}_{4}}$|=2(PE+PF)≥$\frac{20}{3}$,
故选:C.
点评 本题主要考查向坐标的运算和向量模长的计算,根据抛物线的性质,利用构造法抓好为两点间的距离是解决本题的关键.综合性较强.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | [-1,1] | B. | (-∞,-1)∪(1,+∞) | C. | {-1,1} | D. | (-1,1) |
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x>0) | B. | $\frac{x^2}{16}-\frac{y^2}{9}$=1 | C. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x<0) | D. | $\frac{x^2}{25}+\frac{y^2}{9}$=1 |
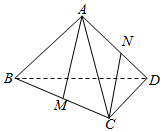 空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )
空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为$\frac{41π}{4}$.
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为$\frac{41π}{4}$.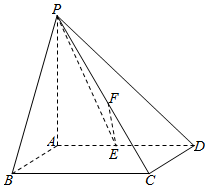 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.