题目内容
已知直线l1：2x-y+3=0和直线l2：x=-1，则抛物线y2=4x上一动点P到直线l1和l2的距离值和的最小值是 ．
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：如图所示，过点P作PN⊥l2，PM⊥l1，垂足分别为N，M．由于直线l2是抛物线y2=4x的准线，可得|PN|=|PF|．当且仅当三点M，P，F共线时动点P到直线l1和l2的距离值和取得最小值|FM|．再利用点到直线的距离公式即可得出．
解答：
解：如图所示，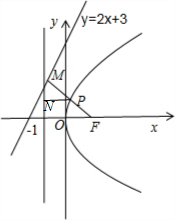
过点P作PN⊥l2，PM⊥l1，垂足分别为N，M．
∵直线l2是抛物线y2=4x的准线，∴|PN|=|PF|．
∴当且仅当三点M，P，F共线时动点P到直线l1和l2的距离值和取得最小值|FM|．
∴最小值|FM|=
=
．
故答案为：
．
过点P作PN⊥l2，PM⊥l1，垂足分别为N，M．
∵直线l2是抛物线y2=4x的准线，∴|PN|=|PF|．
∴当且仅当三点M，P，F共线时动点P到直线l1和l2的距离值和取得最小值|FM|．
∴最小值|FM|=
| |2-0+3| | ||
|
| 5 |
故答案为：
| 5 |
点评：本题考查了抛物线的性质、点到直线的距离公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知AB为圆O的直径，AC与圆O相切于点A，CE∥AB交圆O于D、E两点，若AB=6，BE=2，则线段CD的长为函数f（x）=lnx-
ax2+x有极值且极值大于0，则a的取值范围是（ ）
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（0，2） |
| D、（3，4） |