题目内容
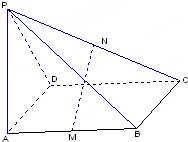如图，在四棱锥P-ABCD中，ABCD是平行四边形，M，N分别是AB，PC的中点，求证：MN∥平面PAD．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：取PD的中点E，连接AE，EN，通过证明MN∥AE．利用直线与平面平行的判定定理证明MN∥平面PAD．
解答：
证明：取PD的中点E，连接AE，EN，
∵N为中点，∴EN为△PDC的中位线，∴EN平行且等于
，
又∵CD平行且等于AB，∴EN平行且等于AM，
∴四边形AMNE为平行四边形，∴MN∥AE．
又∵MN?平面PAD，AE?平面PAD，
∴MN∥平面PAD．
证明：取PD的中点E，连接AE，EN，∵N为中点，∴EN为△PDC的中位线，∴EN平行且等于
| CD |
| 2 |
又∵CD平行且等于AB，∴EN平行且等于AM，
∴四边形AMNE为平行四边形，∴MN∥AE．
又∵MN?平面PAD，AE?平面PAD，
∴MN∥平面PAD．
点评：本题考查直线与平面平行的判定定理的应用，考查空间想象能力以及逻辑推理能力．
练习册系列答案
相关题目