题目内容
要从7个班中选10人参加演讲比赛,每班至少1人,共有 种不同的选法.
考点:排列、组合及简单计数问题
专题:排列组合
分析:根据题意,要从7个班中选10人参加演讲比赛,每班至少1人,可以分为三类,根据分类计数原理可得.
解答:
解:共分三类:
第一类:一个班出4人,其余6个班各出1人,有C
种;
第二类:有2个班分别出2人,3人,其余5个班各出1人,有A
种;
第三类:有3个班各出2人,其余4个班各出1人,有C
种,
故共有C
+A
+C
=84(种).
故答案为:84.
第一类:一个班出4人,其余6个班各出1人,有C
1 7 |
第二类:有2个班分别出2人,3人,其余5个班各出1人,有A
2 7 |
第三类:有3个班各出2人,其余4个班各出1人,有C
3 7 |
故共有C
1 7 |
2 7 |
3 7 |
故答案为:84.
点评:本题主要考查了分类计数原理,如何分类时关键,要不重不漏,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
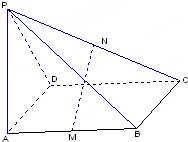 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点,求证:MN∥平面PAD.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点,求证:MN∥平面PAD.