题目内容
已知sin（α-β）cosα-cos（α-β）sinα=
，那么cos2β的值是 ．
| 3 |
| 5 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：根据两角差的正弦公式化简式子，再由诱导公式求出sinβ的值，代入“cos2β=1-2sin2β”求出cos2β的值．
解答：
解：∵sin（α-β）cosα-cos（α-β）sinα=
，
∴sin（α-β-α）=sin（-β）=
，即sinβ=-
，
则cos2β=1-2sin2β=1-2×
=
，
故答案为：
．
| 3 |
| 5 |
∴sin（α-β-α）=sin（-β）=
| 3 |
| 5 |
| 3 |
| 5 |
则cos2β=1-2sin2β=1-2×
| 9 |
| 25 |
| 7 |
| 25 |
故答案为：
| 7 |
| 25 |
点评：本题考查两角差的正弦公式，诱导公式，以及二倍角的余弦公式，熟练掌握公式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
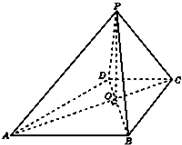如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC，AC⊥BD，AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2，PO=
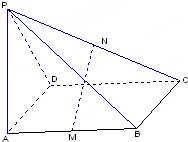如图，在四棱锥P-ABCD中，ABCD是平行四边形，M，N分别是AB，PC的中点，求证：MN∥平面PAD．