题目内容

P为△ABC所在平面上的点，求满足
AB
+
AP
=
1
2
AC
，则△ABP与△ABC的面积之比是
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：根据向量加法的平行四边形法则能够画出△ABC及线段AP，根据图形便较容易求出△ABP与△ABC的面积之比．
解答： 解：设AC中点为D，根据向量加法的平行四边形法则，作出向量
AP
如下图：
S△ABP=S△ABD，S△ABD=
1
2
|AB||AD|sin∠BAD，S△ABC=
1
2
|AB||AC|sin∠BAC；
∵|AD|=
1
2
|AC|，∠BAD=∠BAC，
∴S△ABD：S△ABC=1：2，
即：△ABP与△ABC的面积之比是1：2．
故答案为：1：2．
点评：考查向量加法的平行四边形法则，三角形的面积公式．
练习册系列答案
相关题目
已知f（x）是定义在[-2，2]上的函数，且对任意实数x1，x2（x1≠x2），恒有
f(x1)-f(x2)
x1-x2
＜0，且f（x）的最大值为1，则满足f（log2x）＜1的解集为
 
．
已知二次函数f（x）=ax2-2bx+a，若实数a，b均是从集合{0，1，2，3}中任取的元素（可以重复），则该函数只有一个零点的概率为
 
．
若复数z满足（1+i）z=2i，则复数z=
 
．
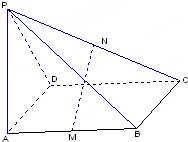如图，在四棱锥P-ABCD中，ABCD是平行四边形，M，N分别是AB，PC的中点，求证：MN∥平面PAD．
x≥0，y≥0，x+y≤4所围成的平面区域的周长是
 
．
给出下列有关命题的四个说法：
①“x2=1”是“x=1”的必要不充分条件；
②p：“y=sinx在第一象限是增函数”；q：“a2+b2≥ab”；则p∧q是真命题；
③命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1≥0”；
④命题“若sinx=siny，则x=y或x=π-y”的逆否命题为真命题．
其中说法正确的有
 
（只填正确的序号）．
已知函数f（x）=asinx+bcosx（x∈R，ab≠0），给出下列命题：
①存在a，b使f（x）是奇函数；
②若对任意x∈R，存在x1，x2，使f（x1）≤f（x）≤f（x2）成立，则|x1-x2|的最小值为π；
③过点（a，b）作直线l，则直线l与函数f（x）=asinx+bcosx（x∈R，ab≠0）的图象必有交点；
④若对任意x∈R，|f（x）|≥|f（
3π
4
）|，则a=b；
⑤若tanα=
a
b
，则f（α）=±
a2+b2
．
其中正确的是
 
（写出所有正确命题的序号）．
如图，各条棱长均为2的正三棱柱ABC-A1B1C1中，M为A1C1的中点，则三棱锥M-AB1C的体积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网