题目内容
12.设椭圆$\frac{{x}^{2}}{10}$+y2=1和双曲线$\frac{{x}^{2}}{8}$-y2=1的公共点为F1,F2,且P是这两曲线的交点,则△PF1F2的外接圆半径为3.分析 利用椭圆、双曲线的定义,结合余弦定理,证明PF1⊥PF2,即可求出△PF1F2的外接圆半径.
解答 解:由题意,|PF1|+|PF2|=2$\sqrt{10}$,|PF1|-|PF2|=2$\sqrt{8}$,
∴|PF1|=$\sqrt{10}$+2$\sqrt{2}$,|PF2|=$\sqrt{10}$-2$\sqrt{2}$,
∵|F1F2|=6,
∴cos∠F1PF2=$\frac{20+16-36}{2(10-8)}$=0,
∴PF1⊥PF2,
∴△PF1F2的外接圆半径为3.
故答案为:3.
点评 本题考查椭圆、双曲线的定义,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2,P是双曲线上的一点,若|PF1|=7,则△PF1F2最大内角的余弦值为( )
| A. | -$\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{59}{117}$ | D. | $\frac{11}{13}$ |
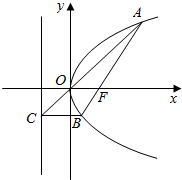 过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.
过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.