题目内容
1．已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2，P是双曲线上的一点，若|PF1|=7，则△PF1F2最大内角的余弦值为（ ）| A． | -$\frac{1}{7}$ | B． | $\frac{1}{7}$ | C． | $\frac{59}{117}$ | D． | $\frac{11}{13}$ |
分析 先求出P在左支上，|PF2|=13，再利用余弦定理求出△PF1F2最大内角的余弦值．
解答 解：双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1中，a=3，b=4，c=5，
∵|PF1|=7，∴P在左支上，|PF2|=13，
∴△PF1F2最大内角的余弦值为$\frac{49+100-169}{2×7×10}$=-$\frac{1}{7}$．
故选：A．
点评 本题考查双曲线的方程与性质，考查余弦定理，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
11．墙上挂着1张高为2m的油画，它的下沿线距地平面2m，观画者的眼睛距地平面1.7m，若使观画者对此画所张的视角达到最大，则他应距墙（ ）m．
| A． | $\sqrt{0.52}$ | B． | $\sqrt{0.34}$ | C． | $\sqrt{0.69}$ | D． | $\sqrt{0.41}$ |
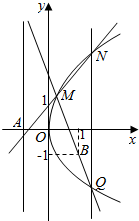如图所示，已知点A（-1，0）是抛物线的准线与x轴的焦点，过点A的直线与抛物线交于M，N两点，过点M的直线交抛物线于另一个点Q，且直线MQ过点B（1，-1）．
6．曲线y=x2在x=0处的（ ）
| A． | 切线斜率为1 | B． | 切线方程为y=2x | C． | 没有切线 | D． | 切线方程为y=0 |