题目内容
4.在△ABC中,若tan$\frac{A}{2}$•tan$\frac{B}{2}$=$\frac{1}{4}$,则tan$\frac{C}{2}$的最大值为$\frac{3}{4}$.分析 利用三角形的内角和,得出$\frac{A}{2}$、$\frac{B}{2}$与$\frac{C}{2}$的关系,再根据三角函数的恒等变换,利用基本不等式,即可得出tan$\frac{C}{2}$的最大值.
解答 解:△ABC中,A+B+C=π,∴$\frac{A+B}{2}$=$\frac{π}{2}$-$\frac{C}{2}$,
∴tan$\frac{A+B}{2}$=tan($\frac{π}{2}$-C)=$\frac{1}{tanC}$,
又tan$\frac{A}{2}$•tan$\frac{B}{2}$=$\frac{1}{4}$,
∴tan$\frac{A+B}{2}$=$\frac{tan\frac{A}{2}+tan\frac{B}{2}}{1-tan\frac{A}{2}•tan\frac{B}{2}}$=$\frac{tan\frac{A}{2}+tan\frac{B}{2}}{1-\frac{1}{4}}$=$\frac{4}{3}$(tan$\frac{A}{2}$+tan$\frac{B}{2}$),
∴tan$\frac{C}{2}$=$\frac{3}{4(tan\frac{A}{2}+tan\frac{B}{2})}$≤$\frac{3}{4×2\sqrt{tan\frac{A}{2}•tan\frac{B}{2}}}$=$\frac{3}{4×2\sqrt{\frac{1}{4}}}$=$\frac{3}{4}$,
tan$\frac{A}{2}$=tan$\frac{B}{2}$=$\frac{1}{2}$“=”成立,
∴tan$\frac{C}{2}$的最大值为$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了三角函数的恒等变换问题,也考查了基本不等式的应用问题,是综合性问题.

| A. | 在三角形ABC中,sinA>sinB,则边a>b | |
| B. | 若对任意正整数n,有a2n+1=an•an+2,则数列{an}为等比数列 | |
| C. | 向量数量积$\overrightarrow{a}$•$\overrightarrow{b}$<0,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角为钝角 | |
| D. | x0为函数y=f(x)的极值点的充要条件是f′(x0)=0 |
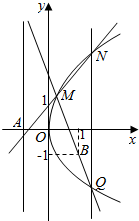 如图所示,已知点A(-1,0)是抛物线的准线与x轴的焦点,过点A的直线与抛物线交于M,N两点,过点M的直线交抛物线于另一个点Q,且直线MQ过点B(1,-1).
如图所示,已知点A(-1,0)是抛物线的准线与x轴的焦点,过点A的直线与抛物线交于M,N两点,过点M的直线交抛物线于另一个点Q,且直线MQ过点B(1,-1).