题目内容
3.a=4,c=$\sqrt{15}$,焦点在y轴上的椭圆的标准方程是$\frac{{y}^{2}}{16}+{x}^{2}=1$.分析 直接求出椭圆的短半轴的长,然后求解椭圆的标准方程即可.
解答 解:a=4,c=$\sqrt{15}$,可得b=1,焦点在y轴上的椭圆的标准方程是:$\frac{{y}^{2}}{16}+{x}^{2}=1$.
故答案为:$\frac{{y}^{2}}{16}+{x}^{2}=1$.
点评 本题考查椭圆的标准方程的求法,基本知识的考查.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
11.墙上挂着1张高为2m的油画,它的下沿线距地平面2m,观画者的眼睛距地平面1.7m,若使观画者对此画所张的视角达到最大,则他应距墙( )m.
| A. | $\sqrt{0.52}$ | B. | $\sqrt{0.34}$ | C. | $\sqrt{0.69}$ | D. | $\sqrt{0.41}$ |
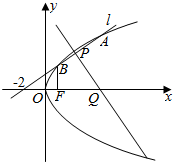 如图,设抛物线y2=4x的焦点为F,过点(-2,0)的直线l交抛物线于A,B两点,线段AB的中垂线分别与AB,x轴交于P,Q两点.若P,Q,F,B四点共圆,则该圆的半径是$\frac{\sqrt{65}}{4}$.
如图,设抛物线y2=4x的焦点为F,过点(-2,0)的直线l交抛物线于A,B两点,线段AB的中垂线分别与AB,x轴交于P,Q两点.若P,Q,F,B四点共圆,则该圆的半径是$\frac{\sqrt{65}}{4}$.