题目内容
已知函数f(x)=alnx-ax-3(a<0).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[0,1],函数g(x)=x3+x2[f′(x)+m]在区间(t,2)上总不是单调函数,其中f′(x)为f(x)的导函数,求实数m的取值范围.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[0,1],函数g(x)=x3+x2[f′(x)+m]在区间(t,2)上总不是单调函数,其中f′(x)为f(x)的导函数,求实数m的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出函数的导数,从而求出单调区间,
(Ⅱ)通过求导求出a的值,从而求出g(x)的表达式,通过解不等式组,求出m的范围.
(Ⅱ)通过求导求出a的值,从而求出g(x)的表达式,通过解不等式组,求出m的范围.
解答:
解 (Ⅰ)根据题意知,f′(x)=
,(x>0),
当a<0时,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:0<x<1
∴f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1].
(Ⅱ)∵f′(2)=-
=1,
∴a=-2,
∴f(x)=-2lnx+2x-3.
∴g(x)=x3+(m+2)x2-2x,
∴g′(x)=3x2+(2m+4)x-2,
∵g(x)在区间(t,2)上总不是单调函数,且g′(0)=-2,
∴
,
由题意知:对于任意的t∈[0,1],g′(t)<0恒成立,
∴
,
∴-
<m<-
.
| a(1-x) |
| x |
当a<0时,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:0<x<1
∴f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1].
(Ⅱ)∵f′(2)=-
| a |
| 2 |
∴a=-2,
∴f(x)=-2lnx+2x-3.
∴g(x)=x3+(m+2)x2-2x,
∴g′(x)=3x2+(2m+4)x-2,
∵g(x)在区间(t,2)上总不是单调函数,且g′(0)=-2,
∴
|
由题意知:对于任意的t∈[0,1],g′(t)<0恒成立,
∴
|
∴-
| 9 |
| 2 |
| 5 |
| 2 |
点评:本题考察了函数的单调性,求参数的范围,导数的应用,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数y=aex+4x(x∈R)有大于零的极值点,则实数a的取值范围是( )
| A、-4<a<0 | ||
| B、a<-4 | ||
C、a<-
| ||
D、-
|
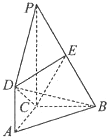 如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.
如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.