题目内容
若x∈[-π,π],为使方程sinx-
cosx=q.
(1)有解;
(2)有两个不同的解;
(3)仅有一解;
请分别求q的值.
| 3 |
(1)有解;
(2)有两个不同的解;
(3)仅有一解;
请分别求q的值.
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:利用三角恒等变换可得q=2sin(x-
),当x∈[-π,π]时,x-
∈[-
,
],利用正弦函数的性质可求得(1)(2)(3)情况下的q的值.
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| 2π |
| 3 |
解答:
解:∵q=sinx-
cosx=2(
sinx-
cosx)=2sin(x-
),
∴当x∈[-π,π]时,x-
∈[-
,
],
∴2sin(x-
)∈[-2,2],
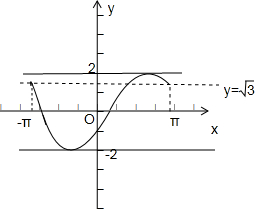
∴(1)q∈[-2,2]时,有解;
(2)当q∈(-2,
)∪(
,2)时,有两个不同的解;
(3)当q=-2或q=2时仅有一解.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴当x∈[-π,π]时,x-
| π |
| 3 |
| 4π |
| 3 |
| 2π |
| 3 |
∴2sin(x-
| π |
| 3 |

∴(1)q∈[-2,2]时,有解;
(2)当q∈(-2,
| 3 |
| 3 |
(3)当q=-2或q=2时仅有一解.
点评:本题考查三角恒等变换与两角和与差的正弦函数,熟练掌握正弦函数的图象与性质是关键,属于中档题.

练习册系列答案
相关题目