题目内容
定义在R上的函数f(x)满足:f(-x)+f(x)=x2,当x<0时,f′(x)<x,则不等式f(x)+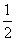 ≥f(1-x)+x的解集为________.
≥f(1-x)+x的解集为________.

[解析] ∵f(x)+f(-x)=x2,∴f′(x)-f′(-x)=2x,∴f′(-x)=f′(x)-2x,
当x<0时,f′(x)<x,∴f′(-x)=f′(x)-2x<x-2x=-x,∴当x>0时,f′(x)=f′(-x)+2x<-x+2x=x,令g(x)=f(x)+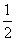 -f(1-x)-x,则g′(x)=f′(x)+f′(1-x)-1<x+1-x-1=0,∴g(x)在R上单调递减,而g
-f(1-x)-x,则g′(x)=f′(x)+f′(1-x)-1<x+1-x-1=0,∴g(x)在R上单调递减,而g =f
=f +
+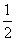 -f
-f -
-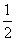 =0,∴g(x)≥0即g(x)≥g
=0,∴g(x)≥0即g(x)≥g ,故原不等式的解集为
,故原不等式的解集为 .
.

练习册系列答案
相关题目
 为等差数列,
为等差数列, ,
, ,则
,则 等于( )
等于( ) A .20
A .20  ,
, 2,
2, 的大小关系是( )
的大小关系是( ) ,则b2b8=( )
,则b2b8=( )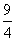 ,底面是边长为
,底面是边长为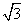 的正三角形,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )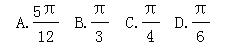
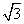 asin B.则角C等于( )
asin B.则角C等于( )