题目内容
若f(x)=(1-x2)(x2+ax+b)的图象关于直线x=2对称,则f(x)的最大值是 .
考点:函数的最值及其几何意义
专题:导数的综合应用
分析:根据对称性求出a,b,利用导数研究函数的最值即可.
解答:
解:∵f(x)=(1-x2)(x2+ax+b)的图象关于直线x=2对称,
∴f(1)=f(3),f(-1)=f(5),
即
,解得a=-8,b=15,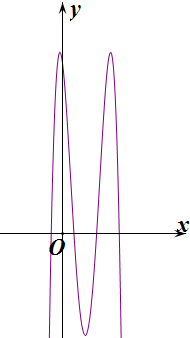
即f(x)=(1-x2)(x2-8x+15)=-x4+8x3-14x2-8x+15,
则f′(x)=-4x3+24x2-28x-8=-4(x-2)(x2-4x-1),
由f′(x)=0,解得x=2或x=2+
或x=2-
,
由f′(x)>0,解得2<x<2+
或x<2-
,此时函数单调递增,
由f′(x)<0,解得2-
<x<2或x>2+
,此时函数单调递减,
作出对应的函数图象如图:
则当x=2+
或2+
时,函数f(x)取得极大值同时也是最大值
则f(2+
)=16,
故答案为:16
∴f(1)=f(3),f(-1)=f(5),
即
|

即f(x)=(1-x2)(x2-8x+15)=-x4+8x3-14x2-8x+15,
则f′(x)=-4x3+24x2-28x-8=-4(x-2)(x2-4x-1),
由f′(x)=0,解得x=2或x=2+
| 5 |
| 5 |
由f′(x)>0,解得2<x<2+
| 5 |
| 5 |
由f′(x)<0,解得2-
| 5 |
| 5 |
作出对应的函数图象如图:
则当x=2+
| 5 |
| 5 |
则f(2+
| 5 |
故答案为:16
点评:本题主要考查函数最值的区间,根据对称性求出a,b的值,利用导数研究函数的单调性和函数的最值求法等知识,综合性较强,难度较大.

练习册系列答案
相关题目
在平行四边形ABCD中,AB=4,AD=2,E,F分别是BC,CD的中点,且
•
=-15,则∠ABC=( )
| DE |
| BF |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义在[1-2a,2-a]上的偶函数f(x),当x≥0时,f(x)=x+ex,若f(t)<f(2t-1).则t的取值范围是( )
| A、[-1,1] | ||
| B、[0,1] | ||
C、[
| ||
D、[0,
|