题目内容
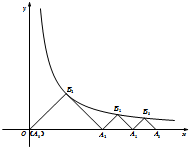 如图,△A0B1A1,△A1B2A2,…,△An-1BnAn均为等腰直角三角形,其直角顶点B1,B2,…,Bn(n∈N*)在曲线y=
如图,△A0B1A1,△A1B2A2,…,△An-1BnAn均为等腰直角三角形,其直角顶点B1,B2,…,Bn(n∈N*)在曲线y=| 1 |
| x |
考点:数列与函数的综合,函数的图象
专题:等差数列与等比数列
分析:由题设知a1=
+
,由此能求出a1,利用△An-1BnAn为等腰直角三角形,且Bn为直角顶点,求出Bn点的横纵坐标,再根据Bn点为函数y=
(x>0)图象上的点,坐标满足函数y=
(x>0)的解析式,就可得到an和an-1 之间的关系式.数列{an2}是首项为4,公差为4的等差数列,由此能求出数列{an}的通项公式.由裂项法,能求出数列{yn}的前n项和Sn.
| a1 |
| 2 |
| 2 |
| a1 |
| 1 |
| x |
| 1 |
| x |
解答:
解:∵曲线y=
上的点与x轴上的点顺次构成等腰直角三角形△OB1A1,△A1B2A2,…,直角顶点在曲线上y=
,设An的坐标为(an,0),A0为原点,
∴a1=
+
,
解得a1=2.
过Bn点作BnH⊥x轴,垂足为H,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴yn=|BnH|=
|An-1An|=
,
∴Bn点的纵坐标为
,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴H点为线段An-1An的中点,
∴H点横坐标为
,
∵BnH⊥x轴,∴Bn点的横坐标也为
,
∵Bn点为函数y=
(x>0)图象上的点,
∴
•
=1
∴an2-an-12=4.
a1=2,
∴数列{an2}是首项为4,公差为4的等差数列,
∴an2=4n,
∴an=2
.
∵yn=
=
=
-
,
∴Sn=(1-
)+(
-1)+…+(
-
)
=
.
故答案为:
.
| 1 |
| x |
| 1 |
| x |
∴a1=
| a1 |
| 2 |
| 2 |
| a1 |
解得a1=2.
过Bn点作BnH⊥x轴,垂足为H,
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴yn=|BnH|=
| 1 |
| 2 |
| an-an-1 |
| 2 |
∴Bn点的纵坐标为
| an-an-1 |
| 2 |
∵△An-1BnAn为等腰直角三角形,且Bn为直角顶点,
∴H点为线段An-1An的中点,
∴H点横坐标为
| an+an-1 |
| 2 |
∵BnH⊥x轴,∴Bn点的横坐标也为
| an+an-1 |
| 2 |
∵Bn点为函数y=
| 1 |
| x |
∴
| an-an-1 |
| 2 |
| an+an-1 |
| 2 |
∴an2-an-12=4.
a1=2,
∴数列{an2}是首项为4,公差为4的等差数列,
∴an2=4n,
∴an=2
| n |
∵yn=
| 2 |
| an+an-1 |
=
| 1 | ||||
|
=
| n |
| n-1 |
∴Sn=(1-
| 0 |
| 2 |
| n |
| n-1 |
=
| n |
故答案为:
| n |
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意数与函数的综合应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
直线x+
y-1=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
“t=1”是“双曲线
-
=1的离心率为2”的( )
| x2 |
| t |
| y2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
不等式(2x-1)(x+1)<0的解集是( )
| A、(-∞,-1) | ||
B、(-1,
| ||
C、(-∞,-1)∪(
| ||
D、(-∞,
|
已知全集U={x∈N|0≤x≤8},U=A∪B,A∩(∁UB)={1,3,5,7},则集合B=( )
| A、{0,2,4} |
| B、{0,2,4,6} |
| C、{0,2,4,6,8} |
| D、{0,1,2,3,4} |
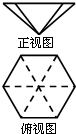 已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为
已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为