题目内容
“t=1”是“双曲线
-
=1的离心率为2”的（ ）
| x2 |
| t |
| y2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义结合双曲线的离心率的公式进行判断即可．
解答：
解：若双曲线
-
=1的离心率为2，
则a2=t＞0，b2=3，c2=t+3，
则e=
=
=2，即
=4，
解得t=1，
故“t=1”是“双曲线
-
=1的离心率为2”的充要条件，
故选：C
| x2 |
| t |
| y2 |
| 3 |
则a2=t＞0，b2=3，c2=t+3，
则e=
| c |
| a |
| ||
|
| t+3 |
| t |
解得t=1，
故“t=1”是“双曲线
| x2 |
| t |
| y2 |
| 3 |
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据双曲线的离心率公式是解决本题的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
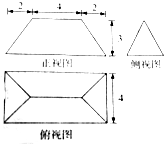
若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（ ）
| A、24cm3 |
| B、40cm3 |
| C、36cm3 |
| D、48cm3 |
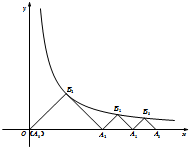如图，△A0B1A1，△A1B2A2，…，△An-1BnAn均为等腰直角三角形，其直角顶点B1，B2，…，Bn（n∈N*）在曲线y=已知全集U={0，1，2，3，4，5，6}，集合A={0，1，2，3}，B={3，4，5}，则（∁UA）∩B=（ ）
| A、{3} |
| B、{4，5} |
| C、{4，5，6} |
| D、{0，1，2} |