题目内容
有甲、已两种商品,经销这两种商品所能获得的利润依次是p万元和q万元,它们与投入的资金x万元的关系有经验公式:p=
x,q=
.现有资金9万元全部投入经销甲、乙两种商品,为了获取最大利润,问:对甲、乙两种商品的资金分别投入多少万元能获得最大利润?
| 1 |
| 10 |
| 2 |
| 5 |
| x |
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:如果设对乙商品投入资金x万元,则对甲投入资金为(9-x)万元,获取的利润为y万元;那么y=p+q,代入可得关于x的解析式,利用换元法得到二次函数f(t),再由二次函数的图象与性质,求导y的最大值,和对应的t、x.
解答:
解:设对乙商品投入资金x万元,则对甲投入资金为(9-x)万元,此时获取利润为y万元;
则由题意知,y=p+q=
(9-x)+
(0≤x≤9).
令
=t,则y=-
(t-2)2+1.3(其中0≤t≤3);
根据二次函数的图象与性质知,当t=2时,y有最大值,为1.3;
又t=2,得x=4(万元),∴9-x=5(万元);
所以,对甲投入资金5万元,对乙投资4万元时,获取利润最大,为1.3万元.
则由题意知,y=p+q=
| 1 |
| 10 |
| 2 |
| 5 |
| x |
令
| x |
| 1 |
| 10 |
根据二次函数的图象与性质知,当t=2时,y有最大值,为1.3;
又t=2,得x=4(万元),∴9-x=5(万元);
所以,对甲投入资金5万元,对乙投资4万元时,获取利润最大,为1.3万元.
点评:本题考查了换元法的应用,运用换元法解题时,要注意换元前后函数自变量取值范围的变化,以免出错.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知角α终边上一点的坐标是(sin
,cos
),则角α的值是( )
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、(-1)k
|
一个几何体的三视图如图所示,则该几何体的正视图面积为( )


| A、2+3π | ||
B、2+
| ||
C、4+
| ||
| D、4+π |
设函数f(x)=2cos2x+
sin2x,x∈R,则下列结论正确的是( )
| 3 |
A、f(x)的图象关于直线x=
| ||
| B、f(x)的最大值是2 | ||
C、f(x)在[0,
| ||
D、f(x)的图象关于点(
|

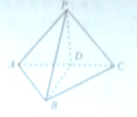 如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.
如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.