题目内容
19．已知函数f（x）=$\left\{\begin{array}{l}{f（x-3），x＞0}\\{{e}^{x}+lo{g}_{2}[{8}^{x+1}×（\frac{1}{4}）^{-2}]，x≤0}\end{array}\right.$，则f（2016）=8．分析 求出函数的周期，利用分段函数的解析式求解函数值即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{f（x-3），x＞0}\\{{e}^{x}+lo{g}_{2}[{8}^{x+1}×（\frac{1}{4}）^{-2}]，x≤0}\end{array}\right.$，
可知x＞0时，函数的周期为3，
则f（2016）=f（0）=e0+log2[81×$（{\frac{1}{4}）}^{-2}$]=1+7=8．
故答案为：8．
点评 本题考查抽象函数的应用以及分段函数的应用，考查计算能力．
练习册系列答案
相关题目
9．若函数f（x）=ln（x+$\sqrt{a+{x}^{2}}$）为奇函数，则a=（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | -1或1 |
10．若双曲线的顶点和焦点分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的焦点和顶点，则该双曲线方程为（ ）
| A． | x2-y2=1 | B． | $\frac{{x}^{2}}{2}$-y2=1 | C． | x2-$\frac{{y}^{2}}{2}$=1 | D． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
14．若f（x）=xex-a有两个零点，则实数a的取值范围是（ ）
| A． | （$\frac{1}{e}$，+∞） | B． | （0，$\frac{1}{e}$） | C． | （-$\frac{1}{e}$，+∞） | D． | （-$\frac{1}{e}$，0） |
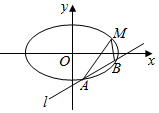⑧如图，已知椭圆的中心在原点，焦点在x轴上，离心率为$\frac{\sqrt{3}}{2}$，且经过点M（4，1），直线l：y=x+m交椭圆与A，B两不同的点．