题目内容
9.已知函数f(x)=tan(ωx-$\frac{π}{5}$)(ω>0)的最小正周期为2π.(Ⅰ)求函数f(x)的定义域;
(Ⅱ)求不等式f(x)>-1的解集.
分析 (Ⅰ)根据正切函数的周期性求得ω的值,可得函数的解析式,从而求得它的定义域.
(Ⅱ)由条件利用正切函数的图象,解三角不等式,求得x的范围.
解答 解:(Ⅰ)由函数f(x)=tan(ωx-$\frac{π}{5}$)(ω>0)的最小正周期为2π,
可得$\frac{π}{ω}$=2π,∴ω=$\frac{1}{2}$,f(x)=tan($\frac{1}{2}$x-$\frac{π}{5}$).
令kπ-$\frac{π}{2}$<$\frac{1}{2}$x-$\frac{π}{5}$<kπ+$\frac{π}{2}$,k∈Z,求得2kπ-$\frac{3π}{5}$<x<2kπ+$\frac{7π}{5}$,
故函数的定义域为(2kπ-$\frac{3π}{5}$,2kπ+$\frac{7π}{5}$),k∈Z.
(Ⅱ)∵不等式f(x)>-1,即tan($\frac{1}{2}$x-$\frac{π}{5}$)>-1,即 kπ-$\frac{π}{4}$<$\frac{1}{2}$x-$\frac{π}{5}$<kπ+$\frac{π}{2}$,
求得 2kπ-$\frac{π}{10}$<x<2kπ+$\frac{7π}{5}$,故不等式的解集为{x|kπ-$\frac{π}{10}$<x<kπ+$\frac{7π}{5}$,k∈Z}.
点评 本题主要考查正切函数的周期性,正切函数的图象,解三角不等式,属于基础题.

练习册系列答案
相关题目
17.三角形的一个内角为60°是这个三角形三内角成等差数列的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
18.不等式($\frac{1}{2}$-x)($\frac{1}{3}$+x)>0的解集为( )
| A. | {x|-$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x<-$\frac{1}{3}$或x>$\frac{1}{2}$} | C. | {x|-$\frac{1}{2}$<x<$\frac{1}{3}$} | D. | {x|x<-$\frac{1}{2}$或x>$\frac{1}{3}$} |
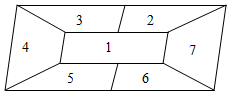 巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.
巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.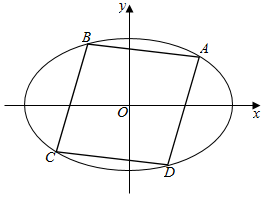 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.