题目内容
求值：
•[
(
•
)-(
•
)
]= ．
| a |
| b |
| a |
| c |
| a |
| b |
| c |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：直接利用向量的数量积的运算法则求解即可．
解答：
解：
•[
(
•
)-(
•
)
]
=
•
(
•
)-(
•
)
•
=0．
故答案为：0．
| a |
| b |
| a |
| c |
| a |
| b |
| c |
=
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
=0．
故答案为：0．
点评：本题考查向量的数量积的运算，考查计算能力．
练习册系列答案
相关题目
已知直线ax+by=0与双曲线
-
=1（0＜a＜b）交于A，B两点，若A（x1，y1），B（x2，y2）满足|x1-x2|=3
，且|AB|=6，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
已知平面向量
，
，|
|=2，
=（2，
），若|
-
|=
，则
在
上的投影为（ ）
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
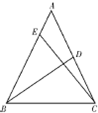如图，在等腰三角形ABC中，底边BC=2，| AD |
| DC |
| AE |
| 1 |
| 2 |
| EB |
| BD |
| AC |
| 1 |
| 2 |
| CE |
| AB |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
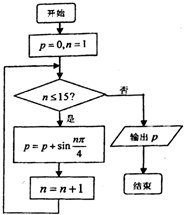
运行如图所示的程序框图后，输出的结果是（ ）
| A、0 | ||||
| B、1 | ||||
C、1+
| ||||
D、1+
|