Question

【题目】选修4-4：坐标系与参数方程

已知直线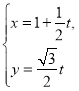：（为参数），曲线：（为参数）．

（1）设与相交于，两点，求；

（2）若把曲线上各点的横坐标压缩为原来的倍，纵坐标压缩为原来的倍，得到曲线，设点是曲线上的一个动点，求它到直线距离的最小值．

Answer 1

【答案】（1）；（2）.

【解析】

试题分析：本题主要考查参数方程的基本性质:（1）将直线和曲线转化为普通方程，联立直线和曲线，求出交点坐标，利用两点间距离公式便可求出；（2）根据坐标变换得出曲线的方程，利用点到直线的距离公式，结合三角函数的最值便可得到点到直线距离的最小值.

试题解析：（1）的普通方程为，的普通方程为，

联立方程组解得与的交点为，，则．

（2）的参数方程为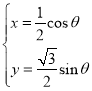（为参数），故点的坐标是，

从而点到直线的距离是，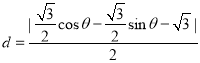

由此当时，取得最小值，且最小值为．