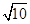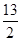题目内容
已知直线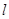 和平面
和平面 ,若
,若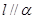 ,
,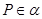 ,过点
,过点 且平行于
且平行于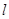 的直线( )
的直线( )
A.只有一条,不在平面 内 内 | B.有无数条,一定在平面 内 内 |
C.只有一条,且在平面 内 内 | D.有无数条,不一定在平面 内 内 |
C
解析试题分析:用反证法证明,由线面平行的性质定理可知,经过直线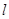 与点
与点 的平面与平面
的平面与平面 的交线
的交线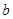 必与直线
必与直线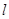 平行.若还存在经过点
平行.若还存在经过点 的另一条直线
的另一条直线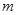 使得
使得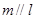 ,则
,则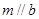 ,又直线
,又直线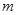 、
、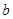 均经过点
均经过点 ,则此情形不可能成立,所以在平面
,则此情形不可能成立,所以在平面 内过点
内过点 只有唯一的一条直线与直线
只有唯一的一条直线与直线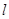 平行.选C.
平行.选C.
考点:空间中线面平行的判定.

练习册系列答案
相关题目
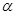 ,
,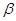 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定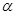 ∥
∥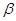 的是( )
的是( )
A.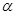 , ,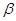 都与平面 都与平面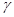 垂直 垂直 |
B.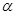 内不共线的三点到 内不共线的三点到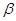 的距离相等 的距离相等 |
C.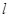 , ,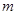 是 是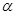 内的两条直线且 内的两条直线且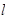 ∥ ∥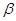 , ,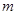 ∥ ∥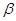 |
D.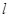 , ,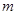 是两条异面直线且 是两条异面直线且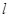 ∥ ∥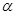 , ,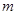 ∥ ∥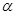 , ,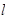 ∥ ∥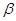 , , 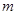 ∥ ∥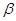 |
如下图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点距离的不同取值有( )
| A.6个 | B.5个 | C.4个 | D.3个 |
已知m和n是两条不同的直线,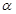 和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
A.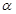 ⊥β且 ⊥β且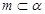 | B.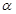 ⊥β且 ⊥β且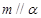 |
C.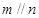 且n⊥β 且n⊥β | D.m⊥n且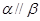 |
如图,在空间直角坐标系中,正方体 的棱长为1,
的棱长为1, ,则
,则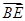 等于( )
等于( )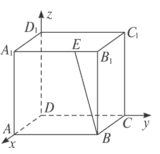
A. | B. 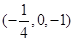 | C. | D.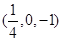 |
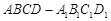 的棱长为
的棱长为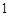 ,
,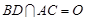 ,
,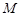 是线段
是线段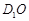 上的动点,过点
上的动点,过点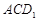 的垂线交平面
的垂线交平面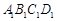 于点
于点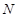 ,则点
,则点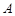 距离的最小值为( )
距离的最小值为( )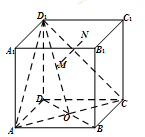

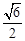
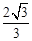



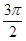

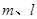 ,平面
,平面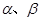 ,且
,且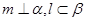 ,给出下列命题:
,给出下列命题: 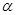 ∥
∥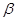 ,则m⊥
,则m⊥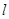 ; ②若
; ②若