题目内容
已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12.则球O的半径为( )
A. | B.2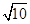 | C.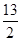 | D.3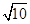 |
C
解析试题分析:因为三棱柱 的6个顶点都在球
的6个顶点都在球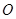 的球面上,
的球面上, ,
, ,
, ,
, ,所以三棱柱的底面是直角三角形,侧棱与底面垂直,侧面
,所以三棱柱的底面是直角三角形,侧棱与底面垂直,侧面 ,经过球的球心,球的直径是其对角线的长,因为
,经过球的球心,球的直径是其对角线的长,因为 ,
, ,
, ,
, ,所以球的半径为:
,所以球的半径为: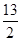 .
.
故选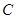 .
.
考点:1.球内接多面体;2.点、线、面间的距离计算.

练习册系列答案
相关题目
已知直线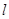 和平面
和平面 ,若
,若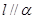 ,
,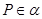 ,过点
,过点 且平行于
且平行于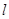 的直线( )
的直线( )
A.只有一条,不在平面 内 内 | B.有无数条,一定在平面 内 内 |
C.只有一条,且在平面 内 内 | D.有无数条,不一定在平面 内 内 |
已知两个不同的平面 和两条不重合的直线
和两条不重合的直线 ,则下列命题不正确的是 ( )
,则下列命题不正确的是 ( )
A.若  则 则 |
B.若  则 则 |
C.若 , ,  ,则 ,则 |
D.若 , , ,则 ,则 |
设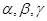 是三个互不重合的平面,
是三个互不重合的平面,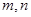 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若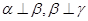 ,则 ,则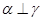 |
B.若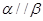 , ,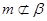 , ,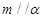 ,则 ,则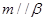 |
C.若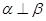 , ,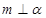 ,则 ,则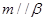 |
D.若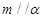 , ,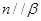 , ,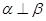 ,则 ,则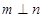 |
正方体ABCD—A1B1C1D1中直线 与平面
与平面 夹角的余弦值是( )
夹角的余弦值是( )
A. | B. | C. | D. |
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
一个棱柱是正四棱柱的条件是( )
| A.底面是正方形,有两个侧面是矩形 |
| B.每个侧面都是全等矩形的四棱柱 |
| C.底面是菱形,且有一个顶点处的三条棱两两垂直 |
| D.底面是正方形,有两个相邻侧面垂直于底面 |
如图,在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中必有( )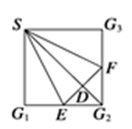
A.SG⊥△EF G所在平面 G所在平面 | B.SD⊥△EFG所在平面 |
C.GF ⊥△SEF所在平面 ⊥△SEF所在平面 | D.GD⊥△SEF所在平面 |
设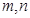 是两条不同的直线,
是两条不同的直线,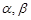 是两个不同的平面,有下列四个命题:
是两个不同的平面,有下列四个命题:
① 若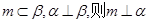 ; ② 若
; ② 若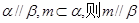 ;
;
③ 若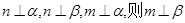 ; ④ 若
; ④ 若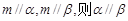
其中正确命题的序号是( )
| A.①③ | B.①② | C.③④ | D.②③ |