题目内容
如下图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点距离的不同取值有( )
| A.6个 | B.5个 | C.4个 | D.3个 |
C
解析试题分析:建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=3,即可得到各顶点的坐标,利用两点间的距离公式即可得出,则A(3,0,0),B(3,3,0),C(0,3,0),D(0,0,0),A1(3,0,3),B1(3,3,3),C1(0,3,3),D1(0,0,3),∴ =(-3,-3,3),设P(x,y,z),∵
=(-3,-3,3),设P(x,y,z),∵ =
=
 =(-1,-1,1),∴
=(-1,-1,1),∴ =
= +(?1,?1,1)=(2,2,1).∴|PA|=|PC|=|PB1|=
+(?1,?1,1)=(2,2,1).∴|PA|=|PC|=|PB1|= =
= ,|PD|=|PA1|
,|PD|=|PA1|
=|PC1|= =3,|PB|=
=3,|PB|= ,|PD1|=
,|PD1|= =2
=2 ,故P到各顶点的距离的不同取值有
,故P到各顶点的距离的不同取值有 ,3,
,3, ,2
,2 ,共4个,故选C.
,共4个,故选C.
考点:点、线、面间的距离计算.

练习册系列答案
相关题目
已知直线 平面
平面 ,直线
,直线
 平面
平面 ,给出下列命题,其中正确的是( )
,给出下列命题,其中正确的是( )
① ②
②
③ ④
④
| A.①③ | B.②③④ | C.②④ | D.①②③ |
设 表示直线
表示直线 表示不同的平面,则下列命题中正确的是( )
表示不同的平面,则下列命题中正确的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若 且 且 ,则 ,则 | D.若 且 且 ,则 ,则 |
下列命题中,错误的是 ( )
| A.一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| B.平行于同一平面的两个不同平面平行 |
C.如果平面 不垂直平面 不垂直平面 ,那么平面 ,那么平面 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面 |
D.若直线 不平行平面 不平行平面 ,则在平面 ,则在平面 内不存在与 内不存在与 平行的直线 平行的直线 |
已知二面角 的平面角是锐角
的平面角是锐角 ,
, 内一点
内一点 到
到 的距离为3,点C到棱
的距离为3,点C到棱 的距离为4,那么
的距离为4,那么 的值等于( )
的值等于( )
A. | B. | C. | D. |
已知直线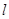 和平面
和平面 ,若
,若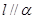 ,
,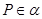 ,过点
,过点 且平行于
且平行于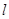 的直线( )
的直线( )
A.只有一条,不在平面 内 内 | B.有无数条,一定在平面 内 内 |
C.只有一条,且在平面 内 内 | D.有无数条,不一定在平面 内 内 |
已知直线m、n和平面α,在下列给定的四个结论中,m∥n的一个必要但不充分条件是( )
| A.m∥α,n∥α | B.m⊥α,n⊥α |
| C.m∥α,n?α | D.m、n与α所成的角相等 |
正方体ABCD—A1B1C1D1中直线 与平面
与平面 夹角的余弦值是( )
夹角的余弦值是( )
A. | B. | C. | D. |
 ,CD=CB=
,CD=CB= ,且
,且 ,现将
,现将 沿着对角线BD翻折成
沿着对角线BD翻折成 ,则在
,则在 内的过程中,直线
内的过程中,直线 与平面
与平面

