题目内容

设F1、F2分别是椭圆
x2
25
+
y2
16
=1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|=3，则P点到椭圆左焦点的距离为（　　）
A、4B、3C、2D、5
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意知，OM是△PF1F2的中位线，由|OM|=3，可得|PF2|=6，再由椭圆的定义求出|PF1|的值．
解答： 解：由题意知，OM是△PF1F2的中位线，
∵|OM|=3，∴|PF2|=6，
又|PF1|+|PF2|=2a=10，
∴|PF1|=4，
故选：A．
点评：本题考查椭圆的定义，以及椭圆的简单性质的应用，判断OM是△PF1F2的中位线是解题的关键，属于中档题．
练习册系列答案
相关题目
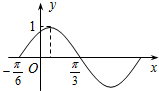某家庭注重家庭理财，从2001年元旦起，每年元旦向银行存款a万元，年利率为r，办理一年定期储蓄，以后按约定自动转存，计算此家庭到2014年元旦去取钱，所得的本利和为多少？
函数f（x）=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜
π
2
)的部分图象如图所示，若x1，x2∈(-
π
6
，
π
3
)，且f（x1）=f（x2）（x1≠x2），则f（x1+x2）=（　　）
A、1
B、
1
2
C、
2
2
D、
3
2
已知函数f（x）=
a
x
+lnx-1（a是常数，e≈=2.71828）．
（1）若x=2是函数f（x）的极值点，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当a=1时，方程f（x）=m在x∈[
1
e
，e2]上有两解，求实数m的取值范围；
（3）求证：n∈N*，ln（en）＞1+
1
2
+
1
3
+…+
1
n
．
已知函数f（x）=3sin（ωx+φ）（ω＞0），若f(
π
3
)=3，f(
π
12
)=0，则ω的最小值为（　　）
A、2B、4C、6D、8
已知函数f（x）=2cosx（sinx-cosx）+1，x∈R
（1）求函数f（x）的单调递增区间；
（2）求函数f（x）在区间[
π
8
，
3π
4
]上的最小值和最大值．
已知{an}是等比数列，对任意n∈N*都有an＞0，如果a3（a3+a5）+a4（a4+a6）=25，则a3+a5=（　　）
A、5B、10C、15D、20
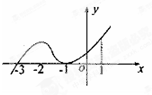如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
①-3是函数y=f（x）的极小值点；
②-1是函数y=f（x）的极值点；
③y=f（x）在x=0处切线的斜率小于零；
④y=f（x）在区间（-3，1）上单调递增．
则正确命题的序号是（　　）
A、①②B、①④C、②③D、③④
如图，两正方形ABCD、ABEF所成二面角大小为120°，求二面角D-AE-B的平面角的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网