题目内容
若点P(x,y)在直线x+y=12上运动,则
+
的最小值为( )
| x2+1 |
| y2+16 |
A、
| ||||
B、
| ||||
| C、13 | ||||
D、1+4
|
考点:两点间距离公式的应用
专题:直线与圆
分析:
+
=
+
,表示x轴上一点P(x,0)到两点A(0,-1),B(12,4)的距离之和,因为AB在x轴两侧,所以P就是直线AB和x轴交点,即可得出结论.
| x2+1 |
| y2+16 |
| (x-0)2+(0+1)2 |
| (x-12)2+(0-4)2 |
解答:
解:∵x+y=12,∴y=12-x
∴
+
=
+
表示x轴上一点P(x,0)到两点A(0,-1),B(12,4)的距离之和
∵△PAB中,两边之和大于第三边,
∴PA+PB>AB
当A、P、B在一直线且P在AB之间时,PAB退化为线段
此时PA+PB=AB,即PA+PB有最小值AB
∵AB在x轴两侧,所以P就是直线AB和x轴交点
∴最小值存在,就是AB距离
=13
故选:C.
∴
| x2+1 |
| y2+16 |
| (x-0)2+(0+1)2 |
| (x-12)2+(0-4)2 |
表示x轴上一点P(x,0)到两点A(0,-1),B(12,4)的距离之和
∵△PAB中,两边之和大于第三边,
∴PA+PB>AB
当A、P、B在一直线且P在AB之间时,PAB退化为线段
此时PA+PB=AB,即PA+PB有最小值AB
∵AB在x轴两侧,所以P就是直线AB和x轴交点
∴最小值存在,就是AB距离
| (0-12)2+(-1-4)2 |
故选:C.
点评:本题考查两点间距离公式的应用,考察学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


A、8+
| ||||
B、8+2
| ||||
| C、12 | ||||
D、
|
已知下列各组命题,其中p是q的充分必要条件的是( )
| A、p:m≤-2或m≥6;q:y=x2+mx+m+3 有两个不同的零点 | ||
B、p:
| ||
| C、p:cosα=cosβ;q:tanα=tanβ | ||
| D、p:A∩B=A; q:A⊆U,B⊆U,∁UB⊆∁UA |
 如图所示,在等腰直角三角形ABC中,AC=AB=2
如图所示,在等腰直角三角形ABC中,AC=AB=2 已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证:
已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证: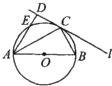 如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为
如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为