题目内容
若圆x2+y2=r2(r>0)上有且只有两个点到直线x-y-2=0的距离为1,则实数r的取值范围是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:到已知直线的距离为1的点的轨迹,是与已知直线平行且到它的距离等于1的两条直线,根据题意可得这两条平行线与x2+y2=r2有2个公共点,由此利用点到直线的距离公式加以计算,可得r的取值范围.
解答:
 解:作出到直线x-y-2=0的距离为1的点的轨迹,得到与直线x-y-2=0平行,且到直线x-y-2=0的距离等于1的两条直线,
解:作出到直线x-y-2=0的距离为1的点的轨迹,得到与直线x-y-2=0平行,且到直线x-y-2=0的距离等于1的两条直线,
∵圆x2+y2=r2的圆心为原点,
原点到直线x-y-2=0的距离为d=
=
,
∴两条平行线中与圆心O距离分别为:
-1,
+1,
如图,当
-1<r<
+1时,圆x2+y2=r2与离圆心较近的直线有两个交点,
即有且只有两个点到直线x-y-2=0的距离为1.
故答案为:(
-1,
+1).
 解:作出到直线x-y-2=0的距离为1的点的轨迹,得到与直线x-y-2=0平行,且到直线x-y-2=0的距离等于1的两条直线,
解:作出到直线x-y-2=0的距离为1的点的轨迹,得到与直线x-y-2=0平行,且到直线x-y-2=0的距离等于1的两条直线,∵圆x2+y2=r2的圆心为原点,
原点到直线x-y-2=0的距离为d=
| |-2| | ||
|
| 2 |
∴两条平行线中与圆心O距离分别为:
| 2 |
| 2 |
如图,当
| 2 |
| 2 |
即有且只有两个点到直线x-y-2=0的距离为1.
故答案为:(
| 2 |
| 2 |
点评:本题给出已知圆上有四点到直线的距离等于半径,求参数的取值范围.着重考查了圆的标准方程、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=sin(2x+φ),其中f(x)≤|f(
)|对x∈R恒成立,且f(
)<f(π),则f(x)的单调递增区间是( )
| π |
| 6 |
| π |
| 2 |
A、[kπ+
| ||||
B、[kπ,kπ+
| ||||
C、[kπ-
| ||||
D、[kπ-
|
已知a,b,c分别为△ABC内角A,B,C的对边,且a,b,c成等比数列,且B=
,则
+
=( )
| π |
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
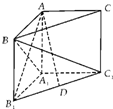 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=AC=AA1. (文科)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将△ADE沿AE折起(D不在平面ABC内).下列说法正确的是
(文科)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将△ADE沿AE折起(D不在平面ABC内).下列说法正确的是