题目内容
为了解我县中学生的体质状况，对天义地区部分中学生进行了身高、体重和肺活量的抽样调查．现随机抽取100名学生，测得其身高情况如下表所示．| 分组 | 频数 | 频率 |
| [155，160） | ① | 0.050 |
| [160，165） | 20 | 0.200 |
| [165，170） | ② | ③ |
| [170，175） | 30 | 0.300 |
| [175，180） | 10 | 0.100 |
| 合计 | 100 | 1.00 |
（2）若按身高分层抽样，抽取20人参加庆“五一”全民健身运动，其中有3名学生参加越野比赛，记这3名学生中“身高低于165cm”的人数为ξ，求ξ的分布列及期望．
考点：离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题：概率与统计
分析：（1）利用频数=频率×容量即可得出，利用频率和为可得③处的频数，利用众数的定义即可得出．根据频率及其纵坐标为
即可补全频率分布直方图．
（2）用分层抽样的方法，从中选取20人，则“身高低于165cm”的有5人．可得ξ的可能的值为0，1，2，3，利用古典概型的概率计算公式即可得出，进而得出分布列及其数学期望．
| 频率 |
| 组距 |
（2）用分层抽样的方法，从中选取20人，则“身高低于165cm”的有5人．可得ξ的可能的值为0，1，2，3，利用古典概型的概率计算公式即可得出，进而得出分布列及其数学期望．
解答：
解：（1）①处的频数=100×0.050=5，同理可得②③处的分别为35、0.350，众数是167.5cm，
补全频率分布直方图；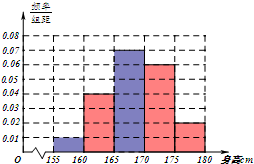
（2）用分层抽样的方法，从中选取20人，则“身高低于165cm”的有5人．
∴ξ的可能的值为0，1，2，3，
则P(ξ=0)=
=
；P(ξ=1)=
=
；
P(ξ=2)=
=
；P(ξ=3)=
=
；
其分布列如下：
Eξ=0×
+1×
+2×
+3×
=
=
．
补全频率分布直方图；
（2）用分层抽样的方法，从中选取20人，则“身高低于165cm”的有5人．
∴ξ的可能的值为0，1，2，3，
则P(ξ=0)=
| ||
|
| 91 |
| 278 |
| ||||
|
| 35 |
| 76 |
P(ξ=2)=
| ||||
|
| 5 |
| 38 |
| ||
|
| 1 |
| 114 |
其分布列如下：
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 91 |
| 278 |
| 35 |
| 76 |
| 5 |
| 38 |
| 1 |
| 114 |
| 57 |
| 76 |
| 3 |
| 4 |
点评：本题考查了频率分布直方图、古典概型的概率计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
中考解读考点精练系列答案
相关题目
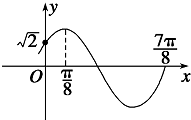函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
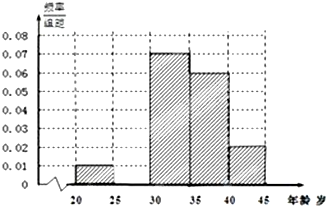某市要对2000多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[20，45）岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示．数列{an}的前n项和记为Sn，a1=1，an+1=2Sn+1（n≥1，n∈N），则数列{an}的通项公式是（ ）
| A、an=2n |
| B、an=2n-1 |
| C、an=3n-1 |
| D、an=3n |
直线y=x与椭圆
+y2=1相交于A，B两点，则|AB|=（ ）
| x2 |
| 4 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|