题目内容
已知函数f(x)=
(1)求f(x)的单调区间;
(2)若关于x的不等式lnx<mx对一切x∈[a,2a](a>0)都成立,求m范围.
| lnx |
| x |
(1)求f(x)的单调区间;
(2)若关于x的不等式lnx<mx对一切x∈[a,2a](a>0)都成立,求m范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)先确定定义域为(0,+∞),求导,则由“f′(x)≥0,为增区间,f′(x)≤0,为减区间”求解.
(2)将“不等式lnx<mx对一切x∈[a,2a](其中a>0)都成立”转化为:m>
,“对一切x∈[a,2a](其中a>0)都成立,”只要求得f(x)在x∈[a,2a](其中a>0)上的最大值即可.
(2)将“不等式lnx<mx对一切x∈[a,2a](其中a>0)都成立”转化为:m>
| lnx |
| x |
解答:
解:(1)定义域为(0,+∞),
∴f′(x)=
,
令f′(x)=0,解得x=e,
当f′(x)>0,解得0<x<e,
当f′(x)<0,解得x>e,
∴f(x)的单调递增区间为(0,e);f(x)的单调递减区间为(e,+∞).
(2)∵不等式lnx<mx对一切x∈[a,2a](其中a>0)都成立,
∴m>
,对一切x∈[a,2a](其中a>0)都成立,
∴下面即求f(x)=
在x∈[a,2a](其中a>0)上的最大值;
∵a>0,由(1)知:f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
当2a≤e时,即0<a≤
时,f(x)在[a,2a]上单调递增,∴f(x)max=f(2a)=
;
当a≥e时,f(x)在[a,2a]上单调递减,∴f(x)max=f(2a)=
;
当a<e<2a时,即
<a<e时,f(x)在[a,e]上单调递增,f(x)在[e,2a]上单调递减,
∴f(x)max=f(e)=
.
综上得:
当0<a≤
时,m>
;
当a≥e时,m>
;
当
<a<e时,m>
.
∴f′(x)=
| 1-lnx |
| x2 |
令f′(x)=0,解得x=e,
当f′(x)>0,解得0<x<e,
当f′(x)<0,解得x>e,
∴f(x)的单调递增区间为(0,e);f(x)的单调递减区间为(e,+∞).
(2)∵不等式lnx<mx对一切x∈[a,2a](其中a>0)都成立,
∴m>
| lnx |
| x |
∴下面即求f(x)=
| lnx |
| x |
∵a>0,由(1)知:f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
当2a≤e时,即0<a≤
| e |
| 2 |
| ln2a |
| 2a |
当a≥e时,f(x)在[a,2a]上单调递减,∴f(x)max=f(2a)=
| lna |
| a |
当a<e<2a时,即
| e |
| 2 |
∴f(x)max=f(e)=
| 1 |
| e |
综上得:
当0<a≤
| e |
| 2 |
| ln2a |
| 2a |
当a≥e时,m>
| lna |
| a |
当
| e |
| 2 |
| 1 |
| e |
点评:本题主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围时,往往转化为求相应函数的最值问题.

练习册系列答案
相关题目
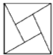 如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形,直角三角形的较短边长为2,向大正方形内投一飞镖,则飞镖落在小正方形内的概率为
如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形,直角三角形的较短边长为2,向大正方形内投一飞镖,则飞镖落在小正方形内的概率为