题目内容
已知函数g(x)对一切实数x,y都有g(x+y)-g(y)=x(x+2y+1)成立,且g(1)=0,设f(x)=
.
(1)求g(0)的值;
(2)求f(x)的解析式.
| g(x)-3x+3 |
| x |
(1)求g(0)的值;
(2)求f(x)的解析式.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)对抽象函数满足的函数值关系的理解和把握是解决该问题的关键,对自变量适当的赋值可以解决该问题,结合已知条件可以赋x=-1,y=1求出f(0);
(2)在(1)基础上赋值y=0可以实现求解f(x)的解析式的问题;
(2)在(1)基础上赋值y=0可以实现求解f(x)的解析式的问题;
解答:
解:(1)∵g(x+y)-g(y)=x(x+2y+1),g(1)=0,
令x=1,y=0,得g(1)-g(0)=1×(1+0+1)=2,
故g(0)=-2,
(2)令y=0,则g(x)-g(0)=x(x+1),
∴g(x)=x2+x-2,
∴f(x)=
=
=x+
-2,
令x=1,y=0,得g(1)-g(0)=1×(1+0+1)=2,
故g(0)=-2,
(2)令y=0,则g(x)-g(0)=x(x+1),
∴g(x)=x2+x-2,
∴f(x)=
| g(x)-3x+3 |
| x |
| x2+x-2-3x+3 |
| x |
| 1 |
| x |
点评:本题考查抽象函数的问题,采用赋值法是解决这类问题的常用方法,属于中档题.

练习册系列答案
相关题目
对于空间中的三条不同的直线,有下列三个条件:
①三条直线两两平行;
②三条直线共点;
③有两条直线平行,第三条直线和这两条直线都相交.
其中,能作为这三条直线共面的充分条件的有( )
①三条直线两两平行;
②三条直线共点;
③有两条直线平行,第三条直线和这两条直线都相交.
其中,能作为这三条直线共面的充分条件的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
实数a,b,c分别满足2a=log
a,(
)b=log
b,(
)c=log2c,则其大小关系为( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<a<c |
若0<x<
,则x(1-2x)有( )
| 1 |
| 2 |
A、最小值
| ||
B、最小值
| ||
C、最大值
| ||
D、最大值
|
已知等差数列{an}的前n项和为Sn,S9=-18,S13=-52,{bn}为等比数列,且b5=a5,b7=a7,则b15的值为( )
| A、64 | B、128 |
| C、-64 | D、-128 |
在△ABC中,∠ABC=60°,AB=2,BC=6,在BC上任取一点D,使△ABD为钝角三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
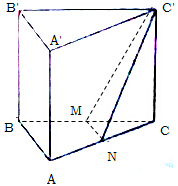 已知三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,侧楼AA1⊥底面ABC,AB=BC=CC1=4,N为AC的中点,M为BC的中点.
已知三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,侧楼AA1⊥底面ABC,AB=BC=CC1=4,N为AC的中点,M为BC的中点.