题目内容
函数f(x)=ex-
的零点所在的区间是( )
| 1 |
| x |
A、(0,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:由条件利用函数的零点的判定定理,可得结论.
解答:
解:函数f(x)=ex-
是(0,+∞)上的增函数,再根据f(
)=
-2<0,f(1)=e-1>0,
可得f(
)f(1)<0,∴函数f(x)=ex-
的零点所在的区间是(
,1),
故选:B.
| 1 |
| x |
| 1 |
| 2 |
| e |
可得f(
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
故选:B.
点评:本题主要考查函数的零点的判定定理的应用,根据函数的解析式求函数的值,判断函数的零点所在的区间的方法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
当0<x<1时,f(x)=
,则下列大小关系正确的是( )
| sinx |
| x |
| A、f2(x)<f(x)<f(x2) |
| B、f(x2)<f2(x)<f(x) |
| C、f(x)<f(x2)<f2(x) |
| D、f2(x)<f(x2)<f(x) |
函数f(x)=xsinx+cosx的导函数原点处的部分图象大致为( )
A、 |
B、 |
C、 |
D、 |
函数f(x)的图象如图所示,则不等式(x+3)•f′(x)<0的解集为( )
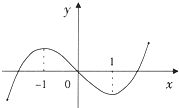

| A、(-∞,-3)∪(-1,1) |
| B、(-∞,-3) |
| C、(-∞,-1)∪(1,+∞) |
| D、(1,+∞) |
函数f(x)=x3-3x2+5的单调减区间是( )
| A、(0,2) |
| B、(0,3) |
| C、(0,1) |
| D、(0,5) |
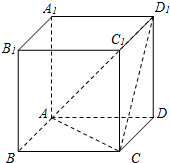 在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是
在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是