题目内容
已知α是第二象限角,且f(α)=
(1)化简f(α);
(2)若cos (α+
)=
,求f(α)的值.
sin(α-
| ||||
| tan(-α-π)sin(-π-α) |
(1)化简f(α);
(2)若cos (α+
| 3π |
| 2 |
| 3 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)直接利用诱导公式化简求解即可.
(2)利用诱导公式化简求值,结合同角三角函数的基本关系式求解即可.
(2)利用诱导公式化简求值,结合同角三角函数的基本关系式求解即可.
解答:
解:(1)f(α)=
=-
=-cosα.
(2)cos(α+
)=
,
可得sinα=
,α是第二象限角,
cosα=-
=-
.
f(α)=-
.
sin(α-
| ||||
| tan(-α-π)sin(-π-α) |
=-
| sinαcosαtanα |
| tanαsinα |
=-cosα.
(2)cos(α+
| 3π |
| 2 |
| 3 |
| 5 |
可得sinα=
| 3 |
| 5 |
cosα=-
| 1-sin2α |
| 4 |
| 5 |
f(α)=-
| 4 |
| 5 |
点评:本题考查诱导公式的应用,三角函数的化简求值考查计算能力.

练习册系列答案
相关题目
下列命题中的假命题是( )
| A、?x∈R,x2>0 | ||
B、?x∈R,tanx=
| ||
| C、?x∈R,lnx=0 | ||
| D、?x∈R,3x>0 |
直线l:2x+3y+6=0的斜率和在y轴上的截距分别为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
复数z=1-i,则
+z对应的点所在的象限为( )
| 1 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若向量
=(1,2),
=(3,4),则
-
=( )
| a |
| b |
| b |
| a |
| A、(4,6) |
| B、(-4,-6) |
| C、(2,2) |
| D、(-2,-2) |
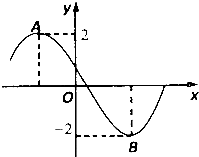 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,