题目内容
13.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( )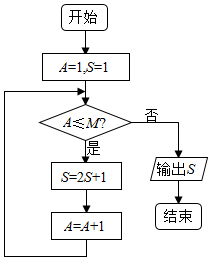
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由图知,每次进入循环体后,S的值被施加的运算是乘以2加上1,由此运算规律进行计算,经过运算后输出的结果是63,从而得解.
解答 解:由图知运算规则是对S=2S+1,执行程序框图,可得
A=1,S=1
满足条件A≤M,第一次进入循环体后S=2×1+1=3,
满足条件A≤M,第二次进入循环体后S=2×3+1=7,
满足条件A≤M,第三次进入循环体后S=2×7+1=15,
满足条件A≤M,第四次进入循环体后S=2×15+1=31,
满足条件A≤M,第五次进入循环体后S=2×31+1=63,
由于A的初值为1,每进入一次循环体其值增大1,第五次进入循环体后A=5.
故判断框中的整数M的值应为5,这样就可保证循环体只能被运行五次.
故选:A.
点评 本题考查循环结构,已知运算规则与最后运算结果,求运算次数的一个题.是算法中一种常见的题型,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
3.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点到一条渐近线的距离不大于$\frac{{\sqrt{5}}}{3}c$(c为双曲线的半焦距长),则双曲线离心率的取值范围为( )
| A. | $[\frac{{3\sqrt{5}}}{2},+∞)$ | B. | $(1,\frac{3}{2}]$ | C. | $(1,\frac{{3\sqrt{5}}}{2}]$ | D. | $[\frac{3}{2},+∞)$ |
8.函数f(x)是定义在(0,+∞)上的单调函数,且对定义域内的任意x,均有f(f(x)-lnx-x3)=2,则f(e)=( )
| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
3.等差数列{an}的首项a1=-5,它的前11项的平均值为5,若从中抽去一项,余下的10项的平均值为4.6,则抽去的是( )
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
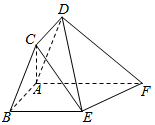 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.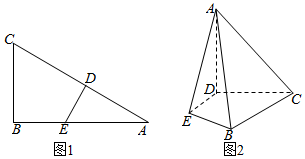 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).