题目内容
已知函数f(x)=
，若方程f（x）-a=0有三个不同的实数根，则a的取值范围为 ．
|
考点：分段函数的应用
专题：函数的性质及应用
分析：根据分段函数f（x）的解析式，作出分段函数的图象，方程f（x）-a=0有三个不同的实数根，即为函数y=f（x）的图象与y=a的图象有三个不同的交点，结合函数的图象即可求得实数a的取值范围．
解答：
解：∵函数f(x)=
，
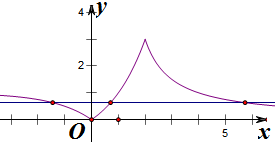
∴作出函数f（x）的图象如右图所示，
∵方程f（x）-a=0有三个不同的实数根，
则函数y=f（x）的图象与y=a的图象有三个不同的交点，
根据图象可知，a的取值范围为0＜a＜1．
故答案为：0＜a＜1．
解：∵函数f(x)=
|
∴作出函数f（x）的图象如右图所示，
∵方程f（x）-a=0有三个不同的实数根，
则函数y=f（x）的图象与y=a的图象有三个不同的交点，
根据图象可知，a的取值范围为0＜a＜1．
故答案为：0＜a＜1．
点评：本题考查了分段函数的应用，考查了分段函数图象的作法．解题的关键在于正确作出函数图象，能将方程f（x）-a=0有三个不同的实数根的问题转化为函数图象有三个不同的交点的问题．解题中综合运用了数形结合和转化化归的数学思想方法．属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知正四面体ABCD的棱长为2，所有与它的四个顶点距离相等的平面截这个四面体所得截面的面积之和是
（ ）
（ ）
A、3+
| ||
| B、4 | ||
| C、3 | ||
D、
|
不等式lgx2＞lg2x的解集是（ ）
| A、（1，100） | ||
| B、（100，+∞） | ||
| C、（0，1）∪（100，+∞） | ||
D、(
|
若f（x）为R上的奇函数，且满足f（x+3）=f（x），当x∈（0，1]时，f（x）=2x，则f（2013）=（ ）
| A、-2 | ||
| B、0 | ||
C、-
| ||
D、
|