题目内容
求函数y=|x2-5x+6|在x∈[-1,a]上的值域.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:先将函数的绝对值符号去掉,化成分段函数,然后给出该函数的单调区间,再讨论函数在[-1,a]上的单调性,从而求出该函数的在区间[-1,a]上的值域.
解答:
解:原函数可化为f(x)=
,该函数在区间(-∞,2],[
,3]上是减函数;在区间(2,
),(3,+∞)上是增函数.
其图象如图所示:
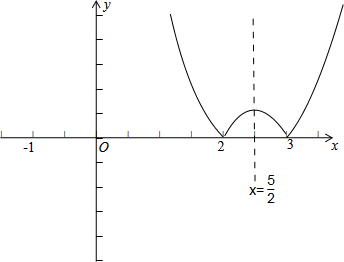
(1)当a≤2时,原函数在[-1,a]上递减,所以ymin=f(a)=a2-5a+6,ymax=f(-1)=12,所以此时值域为[a2-5a+6,12];
(2)当2<a≤6时,因为f(
)=
<f(-1)=f(6)=12,所以由图象可知,函数f(x)在区间[-1,a]上的最小值为0,最大值为f(-1)=12,所以此时值域为[0,12];
(3)当a>6时,结合(2)可知以及图象可知,ymin=0,ymax=f(a)=a2-5a+6,所以此时值域为[0,a2-5a+6].
综上可知,当a≤2时,值域为[a2-5a+6,12];当2<a≤6时,值域为[0,12];当a>6时,值域为[0,a2-5a+6].
|
| 5 |
| 2 |
| 5 |
| 2 |
其图象如图所示:

(1)当a≤2时,原函数在[-1,a]上递减,所以ymin=f(a)=a2-5a+6,ymax=f(-1)=12,所以此时值域为[a2-5a+6,12];
(2)当2<a≤6时,因为f(
| 5 |
| 2 |
| 1 |
| 4 |
(3)当a>6时,结合(2)可知以及图象可知,ymin=0,ymax=f(a)=a2-5a+6,所以此时值域为[0,a2-5a+6].
综上可知,当a≤2时,值域为[a2-5a+6,12];当2<a≤6时,值域为[0,12];当a>6时,值域为[0,a2-5a+6].
点评:本题考查了利用函数单调性求函数值域的方法,关键是利用如何画出函数的图象,进一步研究该函数的单调性.让学生充分体会数形结合的思想在研究函数性质时的作用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图所示的程序是用来( )


| A、计算3×10的值 |
| B、计算39值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
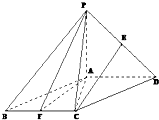 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=