题目内容
如图所示的程序是用来( )


| A、计算3×10的值 |
| B、计算39值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
考点:伪代码
专题:算法和程序框图
分析:写出循环的前三步,根据规律总结出输出的最终结果.
解答:
解:由题意得:
第一步:S=1,i=1≤10成立,
第二步:S=1×3,i=2≤10成立,
第三步:S=1×3×3,i=3≤10不成立,
…
一直到第10步:S=310,i=11>10成立,则输出S=310.
故选:C.
第一步:S=1,i=1≤10成立,
第二步:S=1×3,i=2≤10成立,
第三步:S=1×3×3,i=3≤10不成立,
…
一直到第10步:S=310,i=11>10成立,则输出S=310.
故选:C.
点评:解决此类问题的关键是熟练掌握程序框图的结构特征,即初始值、判断的条件与循环的次数.

练习册系列答案
相关题目
已知f(x)=
,又α,β为锐角三角形的两内角,则( )
|
| A、f(sinα)>f(cosβ) |
| B、f(sinα)<f(cosβ) |
| C、f(sinα)>f(sinβ) |
| D、f(cosα)>f(cosβ) |
运行如图所示的程序框图,若n=2,a1=1,a2=2,则输出的s等于( )


| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是( )
| A、等腰四棱锥的腰与底面所成的角都相等 |
| B、等腰四棱锥的底面四边形必存在外接圆 |
| C、等腰四棱锥的侧面与底面所成的二面角都相等或互补 |
| D、等腰四棱锥的各顶点必在同一球面上 |
已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )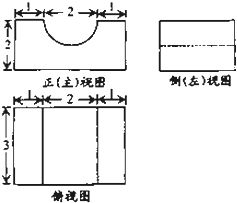

A、24-
| ||||
B、24-
| ||||
| C、24-π | ||||
D、24-
|
若函数g(x)=log3(ax2+2x-1)有最大值1,则实数a的值等于( )
A、-
| ||
B、
| ||
C、-
| ||
| D、4 |