题目内容
已知偶函数y=f(x)定义域是[-3,3],当x≥0时,f(x)=
-1.
(1)求函数y=f(x)的解析式;
(2)画出函数y=f(x)的图象,并利用图象写出函数y=f(x)的单调区间和值域.

| x |
(1)求函数y=f(x)的解析式;
(2)画出函数y=f(x)的图象,并利用图象写出函数y=f(x)的单调区间和值域.

考点:函数图象的作法,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)当x>0时,-x<0,由已知表达式可求f(-x),由偶函数性质可得f(x)与f(-x)的关系;
(2)描点,画图即可,根据图象二次函数的性质分段求出单调区间可得结论;
(2)描点,画图即可,根据图象二次函数的性质分段求出单调区间可得结论;
解答:
解:(1)设x<0,则-x>0.
由y=f(x)是偶函数,得f(x)=f(-x)=
-1,
所以,f(x)=
,
(2)图象如图所示
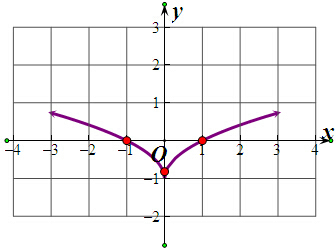
由图象得该函数的单调递减区间是[-
,0],单调递增区间是[0,
].
函数的值域为[-1,
].
由y=f(x)是偶函数,得f(x)=f(-x)=
| -x |
所以,f(x)=
|
(2)图象如图所示

由图象得该函数的单调递减区间是[-
| 3 |
| 3 |
函数的值域为[-1,
| 3 |
点评:本题考查函数解析式的求解及奇偶性的应用,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
计算:4
=( )
| 3 |
| 2 |
| A、2 | B、6 | C、8 | D、12 |