题目内容
已知直三棱柱ABC-A1B1C1，∠C1为直角（1）在直三棱柱ABC-A1B1C1中，若D是AB的中点，求证：AC1∥平面CDB1
（2）在直三棱柱ABC-A1B1C1中，当四边形A1ACC1满足什么条件时，能满足A1B⊥AC1，并加以证明．
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：证明题,空间位置关系与距离
分析：（1）连接BC1交B1C于E，证明AC1∥平面CDB1，只需证明AC1∥DE，利用三角形中位线可得；
（2）当四边形A1ACC1满足AC1⊥A1C时，能满足A1B⊥AC1，证明AC1⊥平面A1BC，即可得出结论．
（2）当四边形A1ACC1满足AC1⊥A1C时，能满足A1B⊥AC1，证明AC1⊥平面A1BC，即可得出结论．
解答：
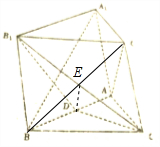（1）证明：连接BC1交B1C于E，∴E为BC1的中点，
连接DE，由D为AB的中点，∴DE为△ABC1的中位线，
∴AC1∥DE，
∵DE?平面CDB1，AC1?平面CDB1，
∴AC1∥平面CDB1；
（2）解：当四边形A1ACC1满足AC1⊥A1C时，能满足A1B⊥AC1，
证明如下：∵BC⊥AC，BC⊥A1A，AC∩A1A=A，
∴BC⊥平面A1ACC1，
∴BC⊥AC1，
∵AC1⊥A1C，A1C∩BC=C，
∴AC1⊥平面A1BC，
∵A1B?平面A1BC，
∴A1B⊥AC1．
（1）证明：连接BC1交B1C于E，∴E为BC1的中点，连接DE，由D为AB的中点，∴DE为△ABC1的中位线，
∴AC1∥DE，
∵DE?平面CDB1，AC1?平面CDB1，
∴AC1∥平面CDB1；
（2）解：当四边形A1ACC1满足AC1⊥A1C时，能满足A1B⊥AC1，
证明如下：∵BC⊥AC，BC⊥A1A，AC∩A1A=A，
∴BC⊥平面A1ACC1，
∴BC⊥AC1，
∵AC1⊥A1C，A1C∩BC=C，
∴AC1⊥平面A1BC，
∵A1B?平面A1BC，
∴A1B⊥AC1．
点评：本题考查线面平行，考查线面垂直，正确利用线面平行、垂直的判定定理是关键．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
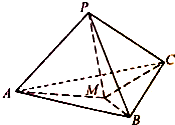如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（