题目内容
11.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的两条渐近线的斜率之积为-2,焦距为6,则双曲线的方程为( )| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B. | $\frac{x^2}{24}$-$\frac{y^2}{12}$=1 | C. | $\frac{x^2}{3}$-$\frac{y^2}{6}$=1 | D. | $\frac{x^2}{6}$-$\frac{y^2}{3}$=1 |
分析 求得双曲线的渐近线方程,由题意可得b=$\sqrt{2}$a,再由c=3,即a2+b2=9,解得a,b,即可得到所求双曲线的方程.
解答 解:双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的两条渐近线方程为
y=±$\frac{b}{a}$x,
由题意可得-$\frac{{b}^{2}}{{a}^{2}}$=-2,
即b=$\sqrt{2}$a,
由2c=6,可得c=3,即a2+b2=9,
解得a=$\sqrt{3}$,b=$\sqrt{6}$,
即有双曲线的方程为$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1.
故选:C.
点评 本题考查双曲线的方程的求法,注意运用渐近线方程和双曲线的基本量的关系,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为锐角三角形,则该双曲线的离心率e的范围是( )
| A. | $(\frac{{\sqrt{6}+\sqrt{2}}}{2},+∞)$ | B. | ($\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{6}+\sqrt{2}}{2}$) | C. | $(\sqrt{6}+\sqrt{2},+∞)$ | D. | $(1,\sqrt{6}+\sqrt{2})$ |
2.已知F1、F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点,过点F2作渐近线的垂线,垂足为点A,若$\overrightarrow{{F_2}A}=2\overrightarrow{AB}$,且点B在以F1为圆心,|OF1|为半径的圆内,则C的离心率取值范围为( )
| A. | $(\sqrt{5},+∞)$ | B. | (2,+∞) | C. | (1,2) | D. | $(1,\sqrt{5})$ |
6.已知关于x的不等式|x+1|≥kx的解集为R,则实数k的取值范围为( )
| A. | k≤0 | B. | -1≤k≤0 | C. | k≥0 | D. | 0≤k≤1 |
16.阅读如图所示的程序框图,若运行该程序后输出的y的值为4,则输入的实数x的值为( )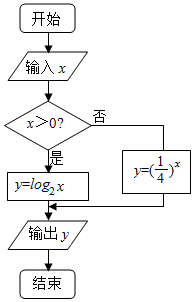

| A. | 4 | B. | 16 | C. | -1或16 | D. | -1或$\frac{1}{16}$ |
3.执行如图所示的程序框图,若输入x=2,则输出的结果为( )


| A. | 2 | B. | 5 | C. | 11 | D. | 23 |
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F(c,0),过F且垂直于x轴的直线在第一象限内与双曲线、双曲线的渐近线的交点依次为A,B,若A为BF的中点,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |