题目内容
3.执行如图所示的程序框图,若输入x=2,则输出的结果为( )
| A. | 2 | B. | 5 | C. | 11 | D. | 23 |
分析 首先分析程序框图,循环体为“直到型”循环结构,按照循环结构进行运算,即可求出满足题意时的y的值.
解答 解:模拟执行程序,可得本程序框图为计算并输出y的值,
循环体为“直到型”循环结构,由框图,可得:
x=2
y=5
不满足条件|x-y|>8,执行循环体,x=5,y=11,
不满足条件|x-y|>8,执行循环体,x=11,y=23,
满足条件|x-y|>8,退出循环,输出y的值为23.
故选:D.
点评 本题为程序框图题,考查对循环结构的理解和认识,按照循环结构运算后得出结果.属于基础题.

练习册系列答案
相关题目
14.已知正数m是2和8的等比中项,则圆锥曲线x2+$\frac{y^2}{m}$=1的焦点坐标为( )
| A. | $(±\sqrt{3},0)$ | B. | $(0,±\sqrt{3})$ | C. | $(±\sqrt{3},0)$或$(±\sqrt{5},0)$ | D. | $(0,±\sqrt{3})$或$(±\sqrt{5},0)$ |
11.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的两条渐近线的斜率之积为-2,焦距为6,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B. | $\frac{x^2}{24}$-$\frac{y^2}{12}$=1 | C. | $\frac{x^2}{3}$-$\frac{y^2}{6}$=1 | D. | $\frac{x^2}{6}$-$\frac{y^2}{3}$=1 |
8.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,点F到渐近线的距离为2a,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 3 |
15.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,图1是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,从左到右各直方块表示的人数依次记为A1、A2、…、A8(例如A2表示血液酒精浓度在30~40mg/100ml的人数),图2是对图1中血液酒精浓度在某一范围内的人数进行统计的程序框图.这个程序框图输出的s=( )
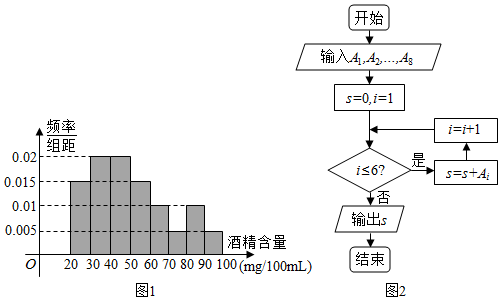

| A. | 24480 | B. | 24380 | C. | 23040 | D. | 23140 |
12.命题“有些相互垂直的两直线不相交”的否定是( )
| A. | 有些相互垂直的两直线相交 | B. | 有些不相互垂直的两直线不相交 | ||
| C. | 任意相互垂直的两直线相交 | D. | 任意相互垂直的两直线不相交 |
13.向量$\overrightarrow{O{Z_1}}$对应的复数是5-4i,向量$\overrightarrow{O{Z_2}}$对应的复数是-5+4i,则向量$\overrightarrow{{Z_1}{Z_2}}$对应的复数是( )
| A. | -10+8i | B. | 10-8i | C. | -8+10i | D. | 8+-10i |