题目内容
已知函数f(x)=ex+alnx的定义域是D,关于函数f(x)给出下列命题:
①对于任意a∈(0,+∞),函数f(x)是D上的减函数;
②对于任意a∈(-∞,0),函数f(x)存在最小值;
③存在a∈(0,+∞),使得对于任意的x∈D,都有f(x)>0成立;
④存在a∈(-∞,0),使得函数f(x)有两个零点.
其中正确命题的序号是( )
①对于任意a∈(0,+∞),函数f(x)是D上的减函数;
②对于任意a∈(-∞,0),函数f(x)存在最小值;
③存在a∈(0,+∞),使得对于任意的x∈D,都有f(x)>0成立;
④存在a∈(-∞,0),使得函数f(x)有两个零点.
其中正确命题的序号是( )
| A、①② | B、②③ | C、②④ | D、③④ |
考点:命题的真假判断与应用
专题:阅读型,导数的综合应用
分析:先求导数,若为减函数则导数恒小于零;在开区间上,若有最小值则有唯一的极小值,若有零点则对应方程有根
解答:
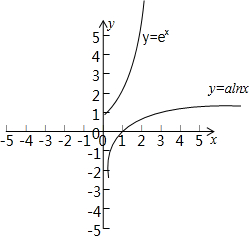 解:由对数函数知:函数的定义域为:(0,+∞),
解:由对数函数知:函数的定义域为:(0,+∞),
f′(x)=ex+
,
①∵a∈(0,+∞)∴f′(x)=ex+
≥0,f(x)是增函数.故①不正确;
②∵a∈(-∞,0),∴存在x有f′(x)=ex+
=0,可以判断函数有最小值,故②正确;
③画出函数y=ex,y=alnx(a>0)的图象,x可取(0,1)内的一个数f(x)<0,故③不正确;
④函数y=ex是增函数,a<0时,y=alnx是减函数,所以存在a∈(-∞,0),由图可让a的绝对值较大,
f(x)=ex+alnx=0有两个根,故④正确.
故选C.
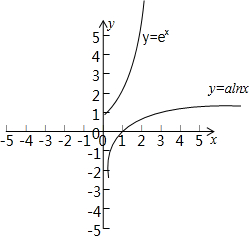 解:由对数函数知:函数的定义域为:(0,+∞),
解:由对数函数知:函数的定义域为:(0,+∞),f′(x)=ex+
| a |
| x |
①∵a∈(0,+∞)∴f′(x)=ex+
| a |
| x |
②∵a∈(-∞,0),∴存在x有f′(x)=ex+
| a |
| x |
③画出函数y=ex,y=alnx(a>0)的图象,x可取(0,1)内的一个数f(x)<0,故③不正确;
④函数y=ex是增函数,a<0时,y=alnx是减函数,所以存在a∈(-∞,0),由图可让a的绝对值较大,
f(x)=ex+alnx=0有两个根,故④正确.
故选C.
点评:本题主要考查导数法研究函数的单调性、极值、最值等问题,注意应用数形结合思想方法,是一道中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
在△ABC中,asinAsinB+bcos2A=
a,则
等于( )
| 2 |
| b |
| a |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
角α的终边落在y=-x(x>0)上,则sinα的值等于( )
A、-
| ||||
B、
| ||||
C、±
| ||||
D、±
|
已知定义在R上的函数f(x)满足:f(x)=
且f(x)=f(x-2),g(x)=
,则方程f(x)=g(x)在区间[-1,5]上的所有实根之和为( )
|
| 2x-3 |
| x-2 |
| A、5 | B、6 | C、7 | D、8 |
若关于x的一元二次方程x2-(m+1)x-m=0有两个异号实数根,则实数m的取值范围是( )
| A、m<0 |
| B、m>0 |
| C、-1<m<1 |
| D、m≥1或m≤-1 |