题目内容

13．设f（x）=$\left\{\begin{array}{l}{sin2x，x＜0}\\{k-1，x≥0}\end{array}\right.$，问当k为何值时，函数f（x）在x=0点连续？

分析 当x=0时，sin2x=sin0=0，若函数f（x）在x=0点连续，则k-1=0，解得答案．

解答 解：当x=0时，f（0）=k-1，
当x=0时，sin2x=sin0=0，
若函数f（x）在x=0点连续，
则k-1=0，
解得：k=1．

点评 本题考查的知识点是分段函数的应用，函数的连续性，难度不大，属于基础题．

练习册系列答案
相关题目
3．已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合．曲线C的参数方程为$\left\{\begin{array}{l}{x=3cosφ}\\{y=2sinφ}\end{array}\right.$（φ为参数），直线l的极坐标方程是ρ（cosθ+2sinθ）=15．若点P、Q分别是曲线C和直线l上的动点，则P、Q两点之间距离的最小值是（　　）
A．$\sqrt{10}$B．2$\sqrt{3}$C．2$\sqrt{5}$D．$\sqrt{21}$
4．函数f（x）=$\frac{{9}^{x}-a}{{3}^{x}}$的图象关于原点对称，则a=（　　）
A．1B．-1C．-$\frac{1}{2}$D．$\frac{1}{2}$
1．把函数g（x）=sin（x-$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位可以得到函数f（x）的图象，则f（$\frac{π}{6}$）=（　　）
A．-$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．-1D．1
8．已知函数f（x）=ex-x2+2ax．
（1）若a=1，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若f（x）在R上单调递增，求实数a的取值范围．
18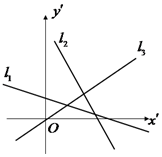．如图，在平面直角坐标系中有三条直线l1，l2，l3，其对应的斜率分别为k1，k2，k3，则下面选项中正确的是（　　）
A．k3＞k1＞k2B．k1-k2＜0C．k2•k3＞0D．k3＞k2＞k1
5．已知向量$\overrightarrow{a}$=（k，3），$\overrightarrow{b}$=（1，4），$\overrightarrow{c}$=（2，1）且（3$\overrightarrow{a}$-2$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则实数k=（　　）
A．-$\frac{9}{2}$B．0C．3D．$\frac{1}{2}$
2．已知函数y=f（x）的定义域为[-1，1]，且f（-x）=-f（x），f（0）=1，当a，b∈[-1，1]且a+b≠0，时$\frac{f（a）+f（b）}{a+b}$＞0恒成立．
（1）判断f（x）在[-1，1]上的单调性并证明结论；
（2）解不等式f（x+$\frac{1}{2}$）＜f（$\frac{1}{x-1}$）
3．一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示．假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km，试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网