题目内容
在平面直角坐标系中,A(0,0),B(1,2)两点绕定点P顺时针方向旋转θ角后,分别到A′(4,4),B′(5,2)两点,则cosθ的值为 .
考点:简单曲线的极坐标方程
专题:三角函数的求值,直线与圆
分析:求出AA′和BB′的中垂线方程,联立得出点P的坐标,然后求出PB与PB′的斜率,利用两条直线所成的角公式求出tanα,即可求出cosα的值.
解答:
 解:由题意,画出图形,如图所示;
解:由题意,画出图形,如图所示;
∵AA′的中点坐标为(2,2),
∴它的中垂线方程:y-2=-(x-2),
即x+y-4=0;
同理BB′的中垂线方程为x=3;
由
,
解得
;
∴点P(3,1)为固定点.
又kPB=
=-
,kPB′=
=
,
∴tanα=
=-
;
∴cosα=-
.
 解:由题意,画出图形,如图所示;
解:由题意,画出图形,如图所示;∵AA′的中点坐标为(2,2),
∴它的中垂线方程:y-2=-(x-2),
即x+y-4=0;
同理BB′的中垂线方程为x=3;
由
|
解得
|
∴点P(3,1)为固定点.
又kPB=
| 2-1 |
| 1-3 |
| 1 |
| 2 |
| 2-1 |
| 5-3 |
| 1 |
| 2 |
∴tanα=
-
| ||||
1+(-
|
| 4 |
| 3 |
∴cosα=-
| 3 |
| 5 |
点评:本题考查了直线方程的应用问题,解题时应根据题意画出图形,结合图形解答问题,是中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
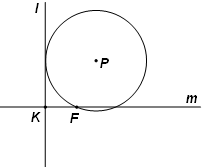 如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.
如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.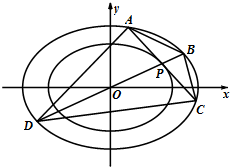 已知曲线C1:
已知曲线C1: