Question

已知椭圆

x2

25

+

y2

9

=1的左焦点为F，点P的坐标为（2，-1），在椭圆上存在一点Q，使|QF|+

4

5

|PQ|的值最小，此最小值为

 

．

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：由椭圆的方程可得椭圆的左准线l：x=-

25

4

，过点Q作QM⊥l交于点M，利用椭圆的第二定义可得

|QF|

|QM|

=

c

a

=

4

5

，因此|QF|=

4

5

|QM|，于是|QF|+

4

5

|PQ|=

4

5

|QM|+

4

5

|PQ|=

4

5

(|QM|+|PQ|)，要使|QF|+

4

5

|PQ|的值最小，当且仅当点P、Q、M三点共线时取得最小值．

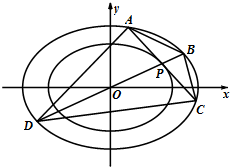
解答： 解：如图所示，由椭圆

x2

25

+

y2

9

=1可得a=5，b=3，c=

a2-b2

=4．
可得椭圆的左准线l：x=-

25

4

，过点Q作QM⊥l交于点M，
由椭圆的第二定义可得

|QF|

|QM|

=

c

a

=

4

5

，
∴|QF|=

4

5

|QM|，
∴|QF|+

4

5

|PQ|=

4

5

|QM|+

4

5

|PQ|=

4

5

(|QM|+|PQ|)，
要使|QF|+

4

5

|PQ|的值最小，当且仅当点P、Q、M三点共线时取得最小值．
∴（|QM|+|PQ|）_min=|PM|=|2-(-

25

4

)|=

33

4

．
因此|QF|+

4

5

|PQ|的最小值=

4

5

×

33

4

=

33

5

，
故答案为：

33

5

．

点评：本题考查了椭圆的定义标准方程及其性质等基础知识，考查了推理能力和计算能力及其转化方法，属于难题．