题目内容
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,…,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品;乙厂执行标准B生产该产品,假定甲、乙两厂的产品都符合相应的执行标准.
(Ⅰ)已知甲厂产品的等级系数X1的概率分布列如表所示:
且X1的数学期望EX1=6,求a,b的值;
(Ⅱ)为分析乙厂产品,从该厂生产的产品中随机抽取10件,相应的等级系数组成一个样本,数据如下:
3 5 4 6 8 5 5 6 3 4,从这10件产品中随机抽取两件(不放回抽样),求这两件产品中符合标准A的产品数ξ的分布列和数学期望.
(Ⅰ)已知甲厂产品的等级系数X1的概率分布列如表所示:
| X1 | 5 | 6 | 7 | 8 |
| P | 0.4 | a | b | 0.1 |
(Ⅱ)为分析乙厂产品,从该厂生产的产品中随机抽取10件,相应的等级系数组成一个样本,数据如下:
3 5 4 6 8 5 5 6 3 4,从这10件产品中随机抽取两件(不放回抽样),求这两件产品中符合标准A的产品数ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)由已知条件推导出0.4+a+b+0.1=1,5×0.4+6a+7b+8×0.1=6,由此能求出a和b.
(Ⅱ)由题意知ξ的所有可能取值为0,1,2,分别求出P(ξ=0),P(ξ=1),P(ξ=2),由此能求出ξ的分布列和Eξ.
(Ⅱ)由题意知ξ的所有可能取值为0,1,2,分别求出P(ξ=0),P(ξ=1),P(ξ=2),由此能求出ξ的分布列和Eξ.
解答:
解:(Ⅰ)由甲厂产品的等级系数X1的概率分布列,知:
0.4+a+b+0.1=1,
∵EX1=6,∴5×0.4+6a+7b+8×0.1=6,
解得a=0.3,b=0.2.
(Ⅱ)由题意知ξ的所有可能取值为0,1,2,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
∴ξ的分布列为:
∴Eξ=0×
+1×
+2×
=
.
0.4+a+b+0.1=1,
∵EX1=6,∴5×0.4+6a+7b+8×0.1=6,
解得a=0.3,b=0.2.
(Ⅱ)由题意知ξ的所有可能取值为0,1,2,
P(ξ=0)=
| ||
|
| 2 |
| 15 |
P(ξ=1)=
| ||||
|
| 8 |
| 15 |
P(ξ=2)=
| ||
|
| 1 |
| 3 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 2 |
| 15 |
| 8 |
| 15 |
| 1 |
| 3 |
| 6 |
| 5 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
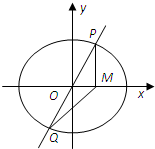 已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为
已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为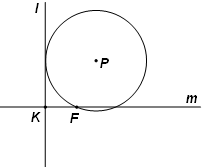 如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.
如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.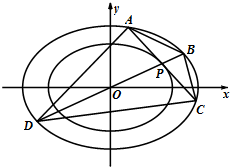 已知曲线C1:
已知曲线C1: